题目内容
2.已知抛物线C:y2=4x的焦点为F.(Ⅰ)点A,P满足$\overrightarrow{AP}$=-2$\overrightarrow{FA}$.当点A在抛物线C上运动时,求动点P的轨迹方程;
(Ⅱ)设斜率为k的直线l过定点P(-2,1),求直线l与抛物线C恰好有一个公共点、两个公共点、没有公共点时k的相应取值范围.
分析 (Ⅰ)求出抛物线的焦点F,设P(x,y),A(x0,y0),求得向量AP,FA的坐标,由条件运用代入法,可得动点P的轨迹方程;
(Ⅱ)由题意可得直线l的方程为y-1=k(x+2),讨论当k=0时,当k≠0时,联立抛物线方程,消去x并整理,由判别式等于0,大于0,小于0,解不等式即可得到所求范围.
解答 解:(Ⅰ)抛物线C:y2=4x的焦点为F(1,0),
设P(x,y),A(x0,y0),则有$y_0^2=4{x_0}$①
$\overrightarrow{AP}=(x-{x_0},y-{y_0})$,$\overrightarrow{FA}=({x_0}-1,{y_0})$.
由$\overrightarrow{AP}=-2\overrightarrow{FA}$,得
$\left\{\begin{array}{l}x-{x_0}=-2({x_0}-1)\\ y-{y_0}=-2{y_0}\end{array}\right.$,即$\left\{\begin{array}{l}{x_0}=2-x\\{y_0}=-y\end{array}\right.$②
把②代入①得动点P的轨迹方程:y2=-4(x-2);
(Ⅱ)由题意可得直线l的方程为y-1=k(x+2),
当k=0时,直线l的方程为y=1,直线l与抛物线C有一个交点;
当k≠0时,由$\left\{\begin{array}{l}y-1=k(x+2)\\{y^2}=4x\end{array}\right.$,消去x并整理,得ky2-4y+8k+4=0.
判别式△=(-4)2-4k(8k+4)=-16(k+1)(2k-1),
由△=0,得k=-1或$k=\frac{1}{2}$;由△>0,得$-1<k<\frac{1}{2}$.
所以,恰好有一个公共点时,k的相应取值范围是$\{-1,0,\frac{1}{2}\}$;
恰好有两个公共点时,k的相应取值范围是$\{x|-1<x<\frac{1}{2},x≠0\}$;
没有公共点时,k的相应取值范围是{x|x<-1,或$x>\frac{1}{2}\}$.
点评 本题考查抛物线的方程和性质,同时考查向量的共线的坐标表示和直线和抛物线的位置关系,考查运算能力,属于中档题和易错题.

计划在某水库建一座至多安装3台发电机的水电站,过去50年的水文资料显示,水库年入流量 (年入流量:一年内上游来水与库区降水之和,单位:亿立方米)都在40以上.其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年.将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(年入流量:一年内上游来水与库区降水之和,单位:亿立方米)都在40以上.其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年.将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(Ⅰ)求在未来4年中,至多1年的年入流量超过120的概率;
(Ⅱ)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量 限制,并有如下关系;
限制,并有如下关系;
年入流量 |
|
|
|
发电机最多可运行台数 | 1 | 2 | 3 |
若某台发电机运行,则该台发电机年利润为5000万元;若某台发电机未运行,则该台发电机年亏损800万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
| A. | $\frac{1}{2}$ | B. | 2 | C. | 4 | D. | 8 |
| A. | 1 | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
| A. | {0,1,3,4} | B. | {1,2,3} | C. | {0,4} | D. | {0} |
 为递增的等比数列,且
为递增的等比数列,且 ,数列
,数列 是等差数列,且
是等差数列,且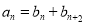 .
. ,
, 的通项公式;
的通项公式; ,求数列
,求数列 得前项和数列
得前项和数列 .
.


 的共轭复数记作
的共轭复数记作 ,已知
,已知 ,(其中i为虚数单位),则复数
,(其中i为虚数单位),则复数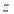 在坐标平面内对应的点在( )
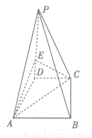
在坐标平面内对应的点在( ) 中,
中, 底面
底面 ,底面
,底面 是直角梯形,
是直角梯形, .
.
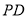 上确定一点
上确定一点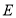 ,使得
,使得 平面
平面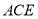 ,并求
,并求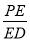 的值;
的值; 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.