题目内容
10.已知双曲线C与双曲线$\frac{x^2}{9}-\frac{y^2}{16}=1$有共同的渐近线,且C经过点$M(-3,2\sqrt{3})$,则双曲线C的实轴长为3.分析 由双曲线C与双曲线$\frac{x^2}{9}-\frac{y^2}{16}=1$有共同的渐近线,设出方程,把点$M(-3,2\sqrt{3})$,代入求出λ再化简即可.
解答 解:由题意双曲线C与双曲线$\frac{x^2}{9}-\frac{y^2}{16}=1$有共同的渐近线,设所求的双曲线的方程为$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{16}=λ$(λ≠0),
因为且C经过点$M(-3,2\sqrt{3})$,所以1-$\frac{3}{4}$=λ,即λ=$\frac{1}{4}$,
代入方程化简得,$\frac{{x}^{2}}{\frac{9}{4}}-\frac{{y}^{2}}{4}=1$,双曲线C的实轴长为:3.
故答案为:3.
点评 本题考查双曲线特有的性质:渐近线,熟练掌握双曲线有共同渐近线的方程特点是解题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
20.已知抛物线y2=4x,椭圆$\frac{x^2}{9}+\frac{y^2}{b}=1$,它们有共同的焦点F2,若P是两曲线的一个公共点,且F1是椭圆的另一个焦点,则△PF1F2的面积为( )
| A. | $\sqrt{6}$ | B. | $2\sqrt{6}$ | C. | $\sqrt{3}$ | D. | 2 |
5.阅读如图所示的程序框图,运行相应的程序,若输入n的值为4,则输出S的值为( )
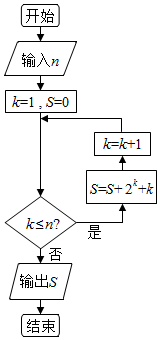

| A. | 20 | B. | 40 | C. | 77 | D. | 546 |
15.倾斜角为60°的直线l过抛物线y2=4x的焦点F,且与抛物线位于x轴上的部分相交于A,则△OFA的面积为( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | $\sqrt{3}$ | D. | $2\sqrt{3}$ |
2.已知函数$f(x)=\frac{1}{2}{x^2}+mlnx-2x$在定义域内是增函数,则实数m的取值范围是( )
| A. | m≤1 | B. | m≥1 | C. | m<1 | D. | m>1 |
 如图,多面体SABCD中面ABCD为矩形,SD⊥AD,且SD⊥AB,AD=a(a>0),AB=2AD,SD=$\sqrt{3}$AD.
如图,多面体SABCD中面ABCD为矩形,SD⊥AD,且SD⊥AB,AD=a(a>0),AB=2AD,SD=$\sqrt{3}$AD.