Question

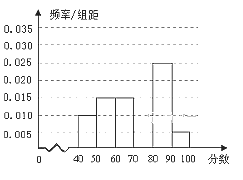
【题目】在某单位的食堂中，食堂每天以10元/斤的价格购进米粉，然后以4.4元/碗的价格出售，每碗内含米粉0.2斤，如果当天卖不完，剩下的米粉以2元/斤的价格卖给养猪场.根据以往统计资料，得到食堂某天米粉需求量的频率分布直方图如图所示，若食堂购进了80斤米粉，以（斤）（其中）表示米粉的需求量， （元）表示利润.

（1）估计该天食堂利润不少于760元的概率；

（2）在直方图的需求量分组中，以区间中间值作为该区间的需求量，以需求量落入该区间的频率作为需求量在该区间的概率，求的分布列和数学期望.

Answer 1

【答案】(1)0.65；(2)答案见解析.

【解析】试题分析：

(1)由题意可得利润函数结合题意求解不等式有即.则食堂利润不少于760元的概率是.

(2)由题意可知可能的取值为460，660，860，960.分别求得相应的概率有， ， ， .据此得出分布列，然后计算数学期望有.

试题解析：

（1）一斤米粉的售价是元.

当时， .

当时， .

故

设利润不少于760元为事件，

利润不少于760元时，即.

解得，即.

由直方图可知，当时，

.

（2）当时， ；

当时， ；

当时， ；

当时， .

所以可能的取值为460，660，860，960.

，

，

，

.

故的分布列为

.