题目内容
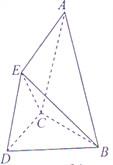
【题目】如图,四棱锥![]() 的底面
的底面![]() 是直角梯形,
是直角梯形, ![]() ,
, ![]() ,
, ![]() ,点
,点![]() 在线段
在线段![]() 上,且
上,且![]() ,
, ![]() ,
, ![]() 平面
平面![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)当四棱锥![]() 的体积最大时,求平面
的体积最大时,求平面![]() 与平面
与平面![]() 所成二面角的余弦值.
所成二面角的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:⑴由条件推出四边形![]() 是矩形,得到
是矩形,得到![]() ,再推出
,再推出![]() ,
, ![]() 平面
平面![]() ,即可推出平面
,即可推出平面![]() 平面
平面![]()
⑵要使四棱锥![]() 的体积取最大值,只需
的体积取最大值,只需![]() 取得最大值,当且仅当
取得最大值,当且仅当![]() 时,
时, ![]() 取得最大值36,分别以
取得最大值36,分别以![]() 所在直线为
所在直线为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,利用向量法求出平面
,利用向量法求出平面![]() 与平面
与平面![]() 所成角的余弦值
所成角的余弦值
解析:(1)由![]() 可得
可得![]() ,
,
易得四边形![]() 是矩形,∴
是矩形,∴![]() ,
,
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() ,
,
又![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]()
(2)四棱锥![]() 的体积为
的体积为![]() ,
,
要使四棱锥![]() 的体积取最大值,只需
的体积取最大值,只需![]() 取得最大值.
取得最大值.
由条件可得![]() ,
,
∴![]() ,即
,即![]() ,
,
当且仅当![]() 时,
时, ![]() 取得最大值36.
取得最大值36.
分别以![]() 所在直线为
所在直线为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() .
.

则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,由
,由![]() ,
, ![]() 可得
可得
![]() ,令
,令![]() 可得
可得![]() ,
,
同理可得平面![]() 的一个法向量为
的一个法向量为![]() ,
,
设平面![]() 与平面
与平面![]() 所成二面角为
所成二面角为![]() ,
,
 .
.
由于平面![]() 与平面
与平面![]() 所成角为锐二面角,所以余弦值为
所成角为锐二面角,所以余弦值为![]() .
.

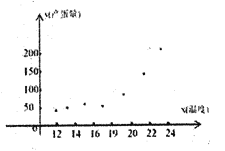
【题目】某市县乡教师流失现象非常严重,为了县乡孩子们能接受良好教育,某市今年要为两所县乡中学招聘储备未来三年的教师,现在每招聘一名教师需要1万元,若三年后教师严重短缺时再招聘,由于各种因素,则每招聘一名教师需要3万元,已知现在该市县乡中学无多余教师,为决策应招聘多少县乡教师搜集并整理了该市50所县乡中学在过去三年内的教师流失数,得到如表的频率分布表:
流失教师数 | 6 | 7 | 8 | 9 |
频数 | 10 | 15 | 15 | 10 |
以这50所县乡中学流失教师数的频率代替一所县乡中学流失教师数发生的概率,记![]() 表示两所县乡中学在过去三年共流失的教师数,
表示两所县乡中学在过去三年共流失的教师数, ![]() 表示今年为两所县乡中学招聘的教师数.为保障县乡孩子教育不受影响,若未来三年内教师有短缺,则第四年马上招聘.
表示今年为两所县乡中学招聘的教师数.为保障县乡孩子教育不受影响,若未来三年内教师有短缺,则第四年马上招聘.
(1)求![]() 的分布列;
的分布列;
(2)若要求![]() ,确定
,确定![]() 的最小值;
的最小值;
(3)以未来四年内招聘教师所需费用的期望值为决策依据,在![]() 与
与![]() 之中选其一,应选用哪个?
之中选其一,应选用哪个?
【题目】随着共享单车的成功运营,更多的共享产品逐步走入大家的世界,共享汽车、共享篮球、共享充电宝等各种共享产品层出不穷.某公司随即抽取![]() 人对共享产品是否对日常生活有益进行了问卷调查,并对参与调查的
人对共享产品是否对日常生活有益进行了问卷调查,并对参与调查的![]() 人中的性别以及意见进行了分类,得到的数据如下表所示:
人中的性别以及意见进行了分类,得到的数据如下表所示:
男 | 女 | 总计 | |
认为共享产品对生活有益 |
|
|
|
认为共享产品对生活无益 |
|
|
|
总计 |
|
|
|
(1)根据表中的数据,能否在犯错误的概率不超过![]() 的前提下,认为对共享产品的态度与性别有关系?
的前提下,认为对共享产品的态度与性别有关系?
(2)现按照分层抽样从认为共享产品增多对生活无益的人员中随机抽取![]() 人,再从
人,再从![]() 人中随机抽取
人中随机抽取![]() 人赠送超市购物券作为答谢,求恰有
人赠送超市购物券作为答谢,求恰有![]() 人是女性的概率.
人是女性的概率.
参与公式: 
临界值表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|