题目内容
已知A(0,2),B(4,6),点P在线段AB(含端点)上运动,求动点P与点Q(1,
)间最小距离.
| 1 |
| 2 |
考点:两点间距离公式的应用
专题:直线与圆
分析:求直线AB的方程,由点到直线的距离公式可得Q到直线的距离,比较AQ和BQ可得.
解答:
解:可得直线AB的斜率k=
=1,
∴直线AB的方程为y=x+2,即x-y+2=0,
∴Q(1,
)到直线AB的距离d=
=
,
又AQ=
=
,
BQ=
>AQ,AQ>
,
∴动点P与点Q(1,
)间最小距离为:
| 6-2 |
| 4-0 |
∴直线AB的方程为y=x+2,即x-y+2=0,
∴Q(1,
| 1 |
| 2 |
|1-
| ||
|
5
| ||
| 4 |
又AQ=
(0-1)2+(2-
|
| ||
| 2 |
BQ=
(4-1)2+(6-
|
5
| ||
| 4 |
∴动点P与点Q(1,
| 1 |
| 2 |
5
| ||
| 4 |
点评:本题考查两点间的距离公式和点到直线的距离公式,属基础题.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
某学校有小学生126人,初中生280人,高中生95人,为了调查学生的近视情况,需要从他们当中抽取一个容量为100的样本,采用何种方法较为恰当( )
| A、简单随机抽样 |
| B、系统抽样 |
| C、分层抽样 |
| D、先从小学生中剔除1人,然后再分层抽样 |
圆心在(a,
),半径为a 的圆的极坐标方程为( )
| π |
| 2 |
| A、ρ=acosθ |
| B、ρ=2acosθ |
| C、ρ=asinθ |
| D、ρ=2asinθ |
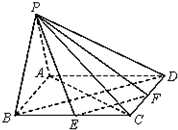 如图,在四棱锥P-ABCD中,四边形ABCD是菱形,PB=PD,且EF分别是BC,CD的中点.求证:
如图,在四棱锥P-ABCD中,四边形ABCD是菱形,PB=PD,且EF分别是BC,CD的中点.求证: