题目内容
对于函数f(x),如果存在区间M=[a,b](a<b),使得{y|y=f(x),x∈M}=M,则称区间M为函数f(x)的一个“稳定区间”.给出下列四个函数:
①f(x)=x3 ②f(x)=ex ③f(x)=lnx+1 ④f(x)=(x-1)2
其中存在“稳定区间”的函数有 .
①f(x)=x3 ②f(x)=ex ③f(x)=lnx+1 ④f(x)=(x-1)2
其中存在“稳定区间”的函数有
考点:函数的值域
专题:函数的性质及应用
分析:根据已知条件可得,要让函数f(x)存在稳定区间,则函数y=x与f(x)的图象至少有两个交点,所以判断给出的四个函数和函数y=x的交点情况即可.
解答:
解:通过已知条件知:若f(x)存在稳定区间,则函数y=x与f(x)图象至少有两个交点;
①f(x)=x3,x∈[-1,1]时,f(x)∈[-1,1],即存在M=[-1,1],使得{y=f(x),x∈M}=M;
即该函数存在稳定区间;
②f(x)=ex,对于x∈[a,b],f(x)∈[ea,eb],通过图象可以看出,y=x与f(x)=ex图象不存在交点,∴该函数不存在稳定区间;

③f(x)=lnx+1,对于x∈[a,b],f(x)∈[lna+1,lnb+1],f(x)的图象是将lnx的图象向上平移1个单位得到,通过图象可以看出y=x与f(x)=lnx+1的图象有2个交点,∴该函数存在稳定区间;

④f(x)=(x-1)2,令y=f(x),解
,得x=
,∴存在区间M=[
,
],使得x∈M,且f(x)∈M,即该函数存在稳定区间.
∴存在“稳定区间”的函数有:①④.
故答案为:①③④.
①f(x)=x3,x∈[-1,1]时,f(x)∈[-1,1],即存在M=[-1,1],使得{y=f(x),x∈M}=M;
即该函数存在稳定区间;
②f(x)=ex,对于x∈[a,b],f(x)∈[ea,eb],通过图象可以看出,y=x与f(x)=ex图象不存在交点,∴该函数不存在稳定区间;

③f(x)=lnx+1,对于x∈[a,b],f(x)∈[lna+1,lnb+1],f(x)的图象是将lnx的图象向上平移1个单位得到,通过图象可以看出y=x与f(x)=lnx+1的图象有2个交点,∴该函数存在稳定区间;

④f(x)=(x-1)2,令y=f(x),解
|
3±
| ||
| 2 |
3-
| ||
| 2 |
3+
| ||
| 2 |
∴存在“稳定区间”的函数有:①④.
故答案为:①③④.
点评:考查函数的定义域,值域,通过图象解决问题以及对稳定区间概念的理解.

练习册系列答案
相关题目
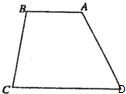 如图所示,有一块四边形的空、地,现欲把它绿化,需知道其面积,以便估算费用.现测得AB=5m,AD=CD=19m,BC=16m,∠ADC=60°.则这块四边形空地的面积是
如图所示,有一块四边形的空、地,现欲把它绿化,需知道其面积,以便估算费用.现测得AB=5m,AD=CD=19m,BC=16m,∠ADC=60°.则这块四边形空地的面积是