题目内容
下列各函数中,最小值为2的是( )
A、y=x+
| ||||
B、y=sinx+
| ||||
C、y=
| ||||
D、y=x+
|
考点:基本不等式
专题:不等式的解法及应用
分析:A.x<0时无最小值;
B.由x∈(0,
),可得sinx∈(0,1),利用基本不等式的性质可得y=sinx+
>2,因此最小值不是2;
C.利用基本不等式的性质可得y>2,因此最小值不是2;
D.由x>1,可得x-1>0.利用基本不等式的性质可得y=x-1+
-2≥2
-2=2.
B.由x∈(0,
| π |
| 2 |
| 1 |
| sinx |
C.利用基本不等式的性质可得y>2,因此最小值不是2;
D.由x>1,可得x-1>0.利用基本不等式的性质可得y=x-1+
| 4 |
| x-1 |
(x-1)•
|
解答:
解:A.x<0时无最小值;
B.∵x∈(0,
),∴sinx∈(0,1),∴y=sinx+
>2
=2,因此最小值不是2;
C.y=
+
>2
=2,因此最小值不是2;
D.∵x>1,∴x-1>0.
∴y=x-1+
-2≥2
-2=2,当且仅当x=3时取等号,因此最小值是2.
故选:D.
B.∵x∈(0,
| π |
| 2 |
| 1 |
| sinx |
sinx•
|
C.y=
| x2+2 |
| 1 | ||
|
|
D.∵x>1,∴x-1>0.
∴y=x-1+
| 4 |
| x-1 |
(x-1)•
|
故选:D.
点评:本题考查了基本不等式的性质,使用时注意“一正二定三相等”的法则,属于基础题.

练习册系列答案
相关题目
在区间(0,1)上随机取两个数u、v,求关于x的一元二次方程x2-
x+u=0有实根的概率为( )
| v |
A、
| ||
B、
| ||
C、
| ||
D、
|
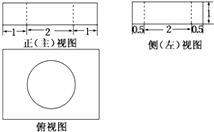
如图是某几何体的三视图,则该几何体的表面积是( )


| A、π | ||
B、
| ||
C、
| ||
| D、4π |
过点P(3,-2)且斜率为2的直线在y轴上的截距是( )
| A、4 | B、-4 | C、8 | D、-8 |