题目内容
19.已知等差数列{an}满足:a3=3,a5+a7=12,{an}的前n项和为Sn.(1)求an及Sn;
(2)令bn=$\frac{1}{{a}_{n}•({a}_{n}+1)}$(n∈N*),求数列{bn}的前10项和T10.
分析 (1)设等差数列{an}的公差为d,运用等差数列的通项公式,可得首项、公差的方程,解方程可得,再由等差数列的通项公式和求和公式即可得到所求;
(2)求得bn=$\frac{1}{{a}_{n}•({a}_{n}+1)}$=$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$,运用数列的求和方法:裂项相消求和,计算即可得到所求和.
解答 解:(1)设等差数列{an}的公差为d,
由a3=3,a5+a7=12,
可得a1+2d=3,a1+4d+a1+6d=12,
解得a1=d=1,
则an=a1+(n-1)d=1+n-1=n,
Sn=$\frac{1}{2}$n(n+1);
(2)bn=$\frac{1}{{a}_{n}•({a}_{n}+1)}$=$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$,
则前10项和T10=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{10}$-$\frac{1}{11}$=1-$\frac{1}{11}$=$\frac{10}{11}$.
点评 本题考查数列的通项公式和求和公式,注意运用等差数列的通项公式,考查方程思想,考查数列的求和方法:裂项相消求和,以及化简整理的运算能力,属于中档题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案
相关题目
11.某工厂拟生产甲、乙两种实销产品.已知每件甲产品的利润为0.4万元,每件乙产品的利润为0.3万元,两种产品都需要在A,B两种设备上加工,且加工一件甲、乙产品在A,B设备上所需工时(单位:h)分别如表所示.
若A设备每月的工时限额为400h,B设备每月的工时限额为300h,则该厂每月生产甲、乙两种产品可获得的最大利润为( )
| 甲产品所需工时 | 乙产品所需工时 | |
| A设备 | 2 | 3 |
| B设备 | 4 | 1 |
| A. | 40万元 | B. | 45万元 | C. | 50万元 | D. | 55万元 |
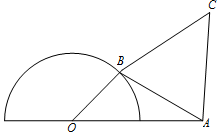 半圆O直径为2,OA=2,B为半圆上任意一点,C为半圆外异于A的点,以AB为边按顺时针方向作正△ABC,问B在何位置时,四边形OACB面积最大?
半圆O直径为2,OA=2,B为半圆上任意一点,C为半圆外异于A的点,以AB为边按顺时针方向作正△ABC,问B在何位置时,四边形OACB面积最大?