题目内容
14．解不等式组：$\left\{\begin{array}{l}\frac{5}{x+3}≥1\\{x^2}+x-2≥0\end{array}$．分析 把要解的不等式组等价转化为$\left\{\begin{array}{l}{-3＜x≤2}\\{x≤-2，或x≥1}\end{array}\right.$，从而求得它的解集．
解答 解：不等式组：$\left\{\begin{array}{l}\frac{5}{x+3}≥1\\{x^2}+x-2≥0\end{array}$，即 $\left\{\begin{array}{l}{0＜x+3≤5}\\{（x+2）•（x-1）≥0}\end{array}\right.$，即 $\left\{\begin{array}{l}{-3＜x≤2}\\{x≤-2，或x≥1}\end{array}\right.$，
求得-3＜x≤-2，或1≤x≤2，
故原不等式组的解集为{x|-3＜x≤-2，或1≤x≤2}．
点评 本题主要考查分式不等式、一元二次不等式的解法，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
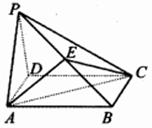如图，在四棱锥P-ABCD中，底面ABCD是边长为2的菱形，且∠ABC=120°，PA=PD，E为PB的中点．