题目内容
6.设f(x)是定义在R上的偶函数,且在(-∞,0]上是增函数,设$a=f({log_4}7),b=f({log_{\frac{1}{2}}}3),c=f({2^{\sqrt{2}}})$,则a,b,c的大小关系是( )| A. | c<a<b | B. | c<b<a | C. | b<c<a | D. | a<b<c |
分析 由偶函数性质得f(x)在[0,+∞)上是减函数,b=f($lo{g}_{\frac{1}{2}}3$)=f(log23),由此利用1<log47<log23=log49<log416=2,${2}^{\sqrt{2}}>{2}^{1}=2$,能判断a,b,c的大小关系.
解答 解:∵f(x)是定义在R上的偶函数,且在(-∞,0]上是增函数,
∴f(x)在[0,+∞)上是减函数,
∵$a=f({log_4}7),b=f({log_{\frac{1}{2}}}3),c=f({2^{\sqrt{2}}})$,
1<log47<log23=log49<log416=2,${2}^{\sqrt{2}}>{2}^{1}=2$,
b=f($lo{g}_{\frac{1}{2}}3$)=f(log23),
∴a,b,c的大小关系是c<b<a.
故选:B.
点评 本题考查三个数的大小的比较,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
相关题目
18.某几何体的三视图如图所示,则其体积为( )


| A. | 207 | B. | $216-\frac{9π}{2}$ | C. | 216-36π | D. | 216-18π |
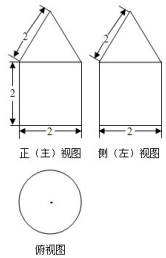 一个几何体的三视图如图所示:
一个几何体的三视图如图所示: