题目内容
6．甲乙丙三人一起参加机动车驾驶证科目考三试后，与丁相聚，丁询问甲乙丙的考试结果，甲说：“我通过了．”，乙说：“我和甲都通过了．”，丙说：“我和乙都通过了．”甲乙丙三人有且只有一个人说的内容与考试结果不完全相同，甲乙丙中没有通过的是丙．分析 分别假设甲和乙的说法考试结果不完全相同，得到矛盾，故可得丙的说法与考试结果不完全相同，再根据甲乙所说判断即可
解答 解：假设甲说的内容与考试结果不完全相同，则甲没有通过，则乙的说法考试结果不完全相同，故甲说的是正确的，
假设乙说的内容与考试结果不完全相同，则甲和乙最多有1人通过，根据丙所说可知乙丙通过了，于是可得甲没有通过，则与甲的说法相矛盾，则乙的说法是正确，
故丙的说法与考试结果不完全相同，于是可得丙没有通过，
故答案为：丙．
点评 本题主要考查简单的合情推理，要抓住关键，逐步推断，是一道基础题．
练习册系列答案
名师点睛字词句段篇系列答案
相关题目
16．若复数z=$\frac{2}{1+i}$+（1-i）2，则|z|等于（ ）
| A． | $\sqrt{10}$ | B． | $\sqrt{2}$ | C． | 2 | D． | $\sqrt{5}$ |
17．下列能正确反映《必修1》中指数幂的推广过程的是（ ）
| A． | 整数指数幂→有理数指数幂→无理数指数幂 | |
| B． | 有理数指数幂→整数指数幂→无理数指数幂 | |
| C． | 整数指数幂→无理数指数幂→有理数指数幂 | |
| D． | 无理数指数幂→有理数指数幂→整数指数幂 |
14．已知向量$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为θ，|$\overrightarrow{OA}$|=2，|$\overrightarrow{OB}$|=1，$\overrightarrow{OP}$=t$\overrightarrow{OA}$，$\overrightarrow{OQ}$=（1-t）$\overrightarrow{OB}$，|$\overrightarrow{PQ}$|在t0时取最小值，当0＜t0＜$\frac{1}{4}$时，cosθ的取值范围为（ ）
| A． | （-$\frac{1}{2}$，0） | B． | （-$\frac{1}{2}$，-$\frac{1}{4}$） | C． | （$\frac{1}{4}$，1） | D． | （-$\frac{1}{2}$，$\frac{1}{4}$） |
1．
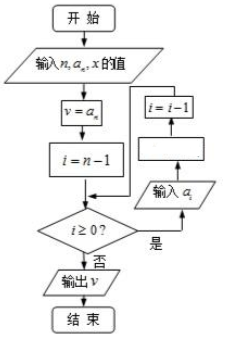我国南宋时期的数学家秦九韶在他的著作《数书九章》中提出了计算多项式f（x）=anxn+an-1xn-1+…+a1x+a0的值的秦九韶算法，即将f（x）改写成如下形式：f（x）=（…（（anx+an-1）x+an-2）x+…+a1）x+a0，首先计算最内层一次多项式的值，然后由内向外逐层计算一次多项式的值，这种算法至今仍是比较先进的算法，将秦九韶算法用程序框图表示如图，则在空白的执行框内应填入（ ）
我国南宋时期的数学家秦九韶在他的著作《数书九章》中提出了计算多项式f（x）=anxn+an-1xn-1+…+a1x+a0的值的秦九韶算法，即将f（x）改写成如下形式：f（x）=（…（（anx+an-1）x+an-2）x+…+a1）x+a0，首先计算最内层一次多项式的值，然后由内向外逐层计算一次多项式的值，这种算法至今仍是比较先进的算法，将秦九韶算法用程序框图表示如图，则在空白的执行框内应填入（ ）| A． | v=vx+ai | B． | v=v（x+ai） | C． | v=aix+v | D． | v=ai（x+v） |
11．有如图所示的程序框图，则该程序框图表示的算法的功能是（ ）
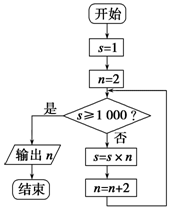
| A． | 输出使1×2×4×…×n≥1 000成立的最大整数n+2 | |
| B． | 输出使1×2×4×…×n≥1 000成立的最小整数n+2 | |
| C． | 输出使1×2×4×…×n≥1 000成立的最小整数n | |
| D． | 输出使1×2×4×…×n≥1 000成立的最大整数n |
18．某几何体的三视图如图所示，则其体积为（ ）
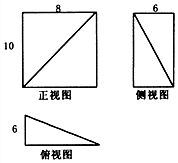
| A． | 80 | B． | 160 | C． | 240 | D． | 480 |
15．已知i是虚数单位，则$\frac{1+i}{1-i}$=（ ）
| A． | 1 | B． | -1 | C． | i | D． | -i |
6．设f（x）是定义在R上的偶函数，且在（-∞，0]上是增函数，设$a=f（{log_4}7），b=f（{log_{\frac{1}{2}}}3），c=f（{2^{\sqrt{2}}}）$，则a，b，c的大小关系是（ ）
| A． | c＜a＜b | B． | c＜b＜a | C． | b＜c＜a | D． | a＜b＜c |