题目内容
1．已知椭圆$\frac{x^2}{25}+\frac{y^2}{9}=1$上一点M到左焦点F1的距离为6，N是MF1的中点，则|ON|=2．分析 利用椭圆的定义及中位线定理即可求得丨ON丨的值．
解答 
解：设椭圆的焦点F2，连结F2M，由M为F1F2的中点，
则ON为三角形F1F2M的中位线，
则丨ON丨=$\frac{1}{2}$丨MF2丨，
由椭圆的定义可知：丨MF1丨+丨MF2丨=2a=10，丨MF1丨=6，
则丨MF2丨=4，
则丨ON丨=2，
故答案为：2．
点评 本题考查椭圆的定义，三角形的中位线定理的应用，考查数形结合思想，属于基础题．
练习册系列答案
备战中考寒假系列答案
相关题目
1．
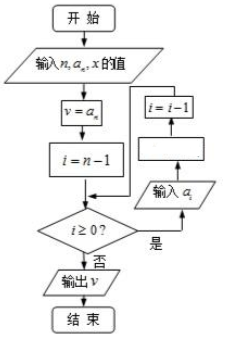我国南宋时期的数学家秦九韶在他的著作《数书九章》中提出了计算多项式f（x）=anxn+an-1xn-1+…+a1x+a0的值的秦九韶算法，即将f（x）改写成如下形式：f（x）=（…（（anx+an-1）x+an-2）x+…+a1）x+a0，首先计算最内层一次多项式的值，然后由内向外逐层计算一次多项式的值，这种算法至今仍是比较先进的算法，将秦九韶算法用程序框图表示如图，则在空白的执行框内应填入（ ）
我国南宋时期的数学家秦九韶在他的著作《数书九章》中提出了计算多项式f（x）=anxn+an-1xn-1+…+a1x+a0的值的秦九韶算法，即将f（x）改写成如下形式：f（x）=（…（（anx+an-1）x+an-2）x+…+a1）x+a0，首先计算最内层一次多项式的值，然后由内向外逐层计算一次多项式的值，这种算法至今仍是比较先进的算法，将秦九韶算法用程序框图表示如图，则在空白的执行框内应填入（ ）| A． | v=vx+ai | B． | v=v（x+ai） | C． | v=aix+v | D． | v=ai（x+v） |
6．设f（x）是定义在R上的偶函数，且在（-∞，0]上是增函数，设$a=f（{log_4}7），b=f（{log_{\frac{1}{2}}}3），c=f（{2^{\sqrt{2}}}）$，则a，b，c的大小关系是（ ）
| A． | c＜a＜b | B． | c＜b＜a | C． | b＜c＜a | D． | a＜b＜c |
10．如图，输入n=5时，则输出的S=（ ）
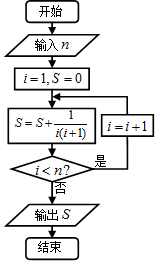
| A． | $\frac{3}{4}$ | B． | $\frac{4}{5}$ | C． | $\frac{5}{6}$ | D． | $\frac{6}{7}$ |