题目内容

18．直线l1与平面α所成的角为30°，直线l2与l1所成角为60°，则l2与平面α所成角的取值范围是[0°，90°]．

分析 l2与平面α所成角的取值范围是就是线面角的范围，线面角的最大值为90°，最小值为0°．

解答 解：∵直线l1与平面α所成的角为30°，直线l2与l1所成角为60°，
∴当l2过l1与α的交点且l2⊥α时，l2与α所成的角最大且为90°；
当l2?α且与l1成60°角时，l2与α所成的角最小且为0°．
∴l2与平面α所成角的取值范围是就是线面角的范围，为[0°，90°]．
故答案为：[0°，90°]．

点评 本题考查直线与平面所成角的取值范围的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．

练习册系列答案
相关题目
8．${（\sqrt{7}-1）^0}-{（\frac{16}{9}）^{-\;\frac{1}{2}}}-{2^{{{log}_2}\frac{1}{3}}}•{log_2}\frac{1}{8}$的值为$\frac{5}{4}$．
9．已知集合A={-2，-1，0，1，2}，B={x|x2-3x-4＜0}，则A∩B=（　　）
A．（-1，1）B．{-1，0，1}C．（0，2）D．{0，1，2}
6．已知0＜x＜1，求f（x）=2+log2x+5logx2的最大值．
13．已知a＞0，且a≠1，求使方程loga（x-ak）=loga$\sqrt{{x}^{2}-{a}^{2}}$有解的k的取值范围．
3．化简：
（1）$\frac{{a}^{-1}+{b}^{-1}}{（ab）^{-1}}$；
（2）$\frac{{a}^{\frac{4}{3}}-8{a}^{\frac{1}{3}}b}{4{b}^{\frac{2}{3}}+2\root{3}{ab}+{a}^{\frac{2}{3}}}$÷（1-2$\root{3}{\frac{b}{a}}$）•$\root{3}{a}$．
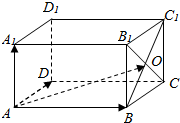10．如图，在平行六面体ABCD-A1B1C1D1中，B1C∩BC1=O，若$\overrightarrow{AO}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$+z$\overrightarrow{A{A}_{1}}$，则x+y+z=2．
7．集合A={x|-2≤x≤5}，B={x|m+1≤x≤2m-1}，
（1）若m=3，求这样的x，使x∈A但x∉B；
（2）当A∩B=∅时，求实数m的取值范围．
8．集合P={x|x2-12＜0}，Q={x|${x}^{\frac{1}{3}}$＞$\frac{1}{2}$，x∈N}，则P∩Q={1，2}．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网