题目内容
6．已知0＜x＜1，求f（x）=2+log2x+5logx2的最大值．分析 根据log2x•logx2=1，利用基本不等式，可得0＜x＜1时，f（x）=2+log2x+5logx2的最大值．
解答 解：∵0＜x＜1，
∴log2x＜0，logx2＜0，
∴-log2x＞0，-5logx2＞0，
∴-log2x-5logx2≥2$\sqrt{（-{log}_{2}x）（-5{log}_{x}2）}$=2$\sqrt{5}$，
故log2x+5logx2≤-2$\sqrt{5}$，
故f（x）=2+log2x+5logx2≤2-2$\sqrt{5}$，
即f（x）=2+log2x+5logx2的最大值为2-2$\sqrt{5}$．
点评 本题考查的知识点是对数的运算性质，基本不等式，函数的最大值，是函数与不等式的综合应用，难度中档．
练习册系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
16．若α∈（0，2π），且tanα＞cotα＞cosα＞sinα，则α的取值范围是（ ）
| A． | （$\frac{π}{4}$，$\frac{π}{2}$） | B． | （$\frac{3π}{4}$，π） | C． | （$\frac{5π}{4}$，$\frac{3π}{2}$） | D． | （$\frac{7π}{4}$，2π） |
14．已知f（x）是定义在R上的奇函数，当0≤x≤1时，f（x）=x2，当x＞0时，f（x+1）=f（x）+f（1），若直线y=kx与函数y=f（x）的图象恰有11个不同的公共点，则实数k的取值范围为（ ）
| A． | （2$\sqrt{2}$-2，2$\sqrt{6}$-4） | B． | （$\sqrt{3}$+2，$\sqrt{3}$+$\sqrt{6}$） | C． | （2$\sqrt{2}$+2，2$\sqrt{6}$+4） | D． | （2$\sqrt{6}$-4，4$\sqrt{3}$-6） |
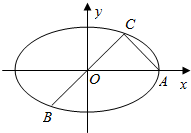如图所示，已知A、B、C是长轴为4的椭圆E上的三点，点A是长轴的一个端点，BC过椭圆中心O，且AC⊥BC，|BC|=2|AC|．