题目内容

8．“ab=0”是“a2+b2=0”的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既充分也不必要条件

分析 根据题意，从2方面进行分析可得：①、若ab=0，则a2+b2=0不一定成立，②、若a2+b2=0，必有a2+b2=0，结合充分必要条件的概念分析可得答案．

解答 解：根据题意，若ab=0，则a=0或b=0，则a2+b2=0不一定成立，如a=0、b=1时，ab=0成立而a2+b2=0不成立，
若a2+b2=0，则有a=b=0，必有a2+b2=0，
故“ab=0”是“a2+b2=0”的必要不充分条件，
故选：B．

点评 本题考查充要条件，解题的关键是正确理解充分、必要条件的含义以及判定方法．

练习册系列答案
相关题目
18．函数f（x）=lg（4-x2）的定义域为（　　）
A．（-∞，-2）∪（2，+∞）B．（-2，2）C．[-2，2]D．（-∞，-2）∪[2，+∞）
19．已知函数f（x）=x2+4[sin（θ+$\frac{π}{3}$）]x-2，θ∈[0，2π]]．
（Ⅰ）若函数f（x）为偶函数，求tanθ的值；
（Ⅱ）若f（x）在[-$\sqrt{3}$，1]上是单调函数，求θ的取值范围．
16．已知$\vec i\;，\;\vec j，\;\vec k$为两两垂直的单位向量，$\overrightarrow{AB}=2\vec i+4\vec j-\vec k$，$\overrightarrow{AC}=-2\vec i+\vec j+\vec k$，则$\overrightarrow{AB}$与$\overrightarrow{AC}$夹角的余弦值为-$\frac{\sqrt{14}}{42}$．
3．在平面直角坐标系xOy中，圆C的方程为x2+y2-8x+15=0．
（1）求直线y=$\frac{1}{3}$x-2被圆截得的弦长；
（2）若直线y=kx-2上至少存在一点，使得以该点为圆心，1为半径的圆与圆C有公共点，求实数k的最大值．
13．已知函数f（x）=excosx，则f（$\frac{π}{6}$）与f（$\frac{π}{5}$）的大小关系是f（$\frac{π}{6}$）＜f（$\frac{π}{5}$）．
20．求方程x2+ax+9=0有实根的充要条件．
17．在2012年奥运选手选拔赛上，8名男运动员参加100米决赛，其中甲、乙、丙三人必须在1、2、3、4、5、6、7、8八条跑道的奇数号跑道上，则安排这8名运动员比赛的方式共有2880种．
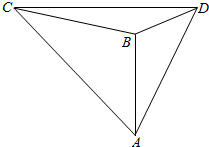18．在某次军事演习中红方为了准确分析战场形势，在两个相距为$\frac{\sqrt{3}a}{2}$的军事基地C和D，测得蓝方两支精锐部队分别在A处和B处，且∠ADB=30°，∠BDC=30°，∠DCA=60°，∠ACB=45°，如图所示，求蓝方这两支精锐部队的距离．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网