题目内容
18.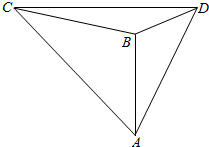 在某次军事演习中红方为了准确分析战场形势,在两个相距为$\frac{\sqrt{3}a}{2}$的军事基地C和D,测得蓝方两支精锐部队分别在A处和B处,且∠ADB=30°,∠BDC=30°,∠DCA=60°,∠ACB=45°,如图所示,求蓝方这两支精锐部队的距离.
在某次军事演习中红方为了准确分析战场形势,在两个相距为$\frac{\sqrt{3}a}{2}$的军事基地C和D,测得蓝方两支精锐部队分别在A处和B处,且∠ADB=30°,∠BDC=30°,∠DCA=60°,∠ACB=45°,如图所示,求蓝方这两支精锐部队的距离.
分析 在△BCD中使用正弦定理求出BC,在△ABC中使用余弦定理求出AB.
解答 解:∵∠BCD=∠DCA-∠ACB=60°-45°=15°,∴∠DBC=180°-∠BDC-∠BCD=135°,
在△BCD中,由正弦定理得:$\frac{CD}{sin∠DBC}=\frac{BC}{sin∠BDC}$,即$\frac{\frac{\sqrt{3}a}{2}}{\frac{\sqrt{2}}{2}}=\frac{BC}{\frac{1}{2}}$,解得BC=$\frac{\sqrt{6}a}{4}$.
∵∠ADC=∠ADB+∠BDC=60°,∠DCA=60°,∴△ACD是等边三角形,∴AC=CD=$\frac{\sqrt{3}a}{2}$.
在△ABC中,由余弦定理得AB2=BC2+AC2-2AB•AC•cos∠ACB=$\frac{3{a}^{2}}{8}$,∴AB=$\frac{\sqrt{6}a}{4}$.
∴蓝方这两支精锐部队的距离为$\frac{\sqrt{6}a}{4}$.
点评 本题考查了正余弦定理在解三角形中的应用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.“ab=0”是“a2+b2=0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既充分也不必要条件 |
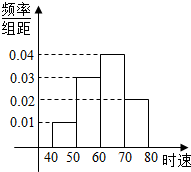 5000辆汽车通过某一段公路时的时速频率分布直方图如图所示.问:
5000辆汽车通过某一段公路时的时速频率分布直方图如图所示.问: