题目内容
4.已知函数f(x)=ax3+bx+1,若f(a)=8,则f(-a)=-6.分析 本题利用函数的奇偶性,得到函数解析式f(-x)与f(x)的关系,从面通过f(-a)的值求出f(a)的值,得到本题结论.
解答 解:∵函数f(x)=ax3+bx+1,
∴f(-x)=a(-x)3+b(-x)+1=-ax3-bx+1,
∴f(-x)+f(x)=2,
∴f(-a)+f(a)=2.
∵f(a)=8,
∴f(a)=-6.
故答案为-6.
点评 本题考查了函数的奇偶性,本题难度不大,属于基础题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
15.已知函数f(x)=sinωx-$\sqrt{3}$cosωx(ω>0),若方程f(x)=-1在(0,π)上有且只有四个实数根,则实数ω的取值范围为( )
| A. | ($\frac{13}{6}$,$\frac{7}{2}$] | B. | ($\frac{7}{2}$,$\frac{25}{6}$] | C. | ($\frac{25}{6}$,$\frac{11}{2}$] | D. | ($\frac{11}{2}$,$\frac{37}{6}$] |
19.已知$\overrightarrow{a}$=(1,cosα),$\overrightarrow{b}$=(sinα,1),0<α<π,若$\vec a⊥\vec b$,则α=( )
| A. | $\frac{2π}{3}$ | B. | $\frac{3π}{4}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
16.已知全集U=R,A={x|x2-2x<0},B={x|2x≥2},则A∩(∁UB)=( )
| A. | {x|0<x<2} | B. | {x|0<x<1} | C. | {x|0<x≤1} | D. | {x|0<x≤2} |
14.“微信抢红包”自2015年以来异常火爆,在某个微信群某次进行的抢红包活动中,若所发红包的总金额为9元,被随机分配为1.49元,1.31元,2.19元,3.40元,0.61元,共5份,供甲、乙等5人抢,每人只能抢一次,则甲、乙二人抢到的金额之和不低于4元的概率是( )
| A. | $\frac{2}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{5}{6}$ |
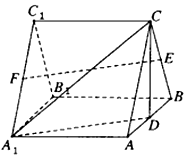 如图,三棱柱ABC-A1B1C1中,各棱长均相等,D,E,F分别为棱AB,BC,A1C1的中点.
如图,三棱柱ABC-A1B1C1中,各棱长均相等,D,E,F分别为棱AB,BC,A1C1的中点.