题目内容
14.“微信抢红包”自2015年以来异常火爆,在某个微信群某次进行的抢红包活动中,若所发红包的总金额为9元,被随机分配为1.49元,1.31元,2.19元,3.40元,0.61元,共5份,供甲、乙等5人抢,每人只能抢一次,则甲、乙二人抢到的金额之和不低于4元的概率是( )| A. | $\frac{2}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{5}{6}$ |
分析 基本事件总数n=${C}_{5}^{2}$=10,再利用列举法求出其中甲、乙二人抢到的金额之和不低于4元的情况种数,帖经能求出甲、乙二人抢到的金额之和不低于4元的概率.
解答 解:所发红包的总金额为10元,被随机分配为1.49元,1.81元,2.19元,3.41元,0.62元,0.48元,
共6份,供甲、乙等6人抢,每人只能抢一次,
基本事件总数n=${C}_{5}^{2}$=10,
其中甲、乙二人抢到的金额之和不低于4元的情况有:
(0.61,3.40),(1.49,3.40),(1.31,3.40),(2.19,3.40),共有4种,
∴甲、乙二人抢到的金额之和不低于4元的概率p=$\frac{4}{10}$=$\frac{2}{5}$.
故选:A.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.为了研究一种昆虫的产卵数y和温度x是否有关,现收集了7组观测数据列于下表中,并作出了散点图,发现样本点并没有分布在某个带状区域内,两个变量并不呈线性相关关系,现分别用模型①:y=C1x2+C2与模型②:y=e${\;}^{{C}_{3}x+{C}_{4}}$作为产卵数y和温度x的回归方程来建立两个变量之间的关系.
其中ti=xi2,$\overline{t}$=$\sum_{i=1}^{7}{t}_{i}$,zi=lnyi,$\overline{u}$=$\sum_{i=1}^{7}{z}_{i}$,
附:对于一组数据(u1,v1),(u2,v2),…,(un,vn),其回归直线v=βu+α的斜率和截距的最小二乘估计分别为:β=$\frac{\sum_{i=1}^{n}({u}_{i}-\overline{u})({v}_{i}-\overline{v})}{\sum_{i=1}^{n}({u}_{i}-\overline{u})^{2}}$,α=$\overline{v}$-β$\overline{u}$.
(1)分别画出y关于t的散点图、z关于x的散点图,根据散点图判断哪一个模型更适宜作为回归方程类型?(给出判断即可,不必说明理由).
(2)根据表中数据,分别建立两个模型下建立y关于x的回归方程;并在两个模型下分别估计温度为30℃时的产卵数.(C1,C2,C3,C4与估计值均精确到小数点后两位)(参考数据:e4.65≈104.58,e4.85≈127.74,e5.05≈156.02)
(3)若模型①、②的相关指数计算分别为R12=0.82,R22=0.96,请根据相关指数判断哪个模型的拟合效果更好.
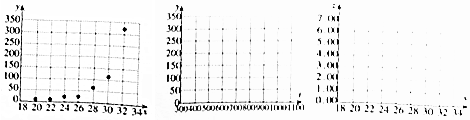
| 温度x/℃ | 20 | 22 | 24 | 26 | 28 | 30 | 32 |
| 产卵数y/个 | 6 | 10 | 21 | 24 | 64 | 113 | 322 |
| t=x2 | 400 | 484 | 576 | 676 | 784 | 900 | 1024 |
| Z=lny | 1.79 | 2.30 | 3.04 | 3.18 | 4.16 | 4.73 | 5.77 |
| $\overline{x}$ | $\overline{t}$ | $\overline{y}$ | $\overline{z}$ |
| 26 | 692 | 80 | 3.57 |
| $\frac{\sum_{i=1}^{7}({x}_{i}-\overline{x})({y}_{i}-\overline{y)}}{\sum_{i=1}^{7}({x}_{i}-\overline{x})^{2}}$ | $\frac{\sum_{i=1}^{7}({t}_{i}-\overline{t})({y}_{i}-\overline{y})}{\sum_{i=1}^{7}({t}_{i}-\overline{t})^{2}}$ | $\frac{\sum_{i=1}^{7}({z}_{i}-\overline{z})({x}_{i}-\overline{x})}{\sum_{i=1}^{7}({x}_{i}-\overline{x})^{2}}$ | $\frac{\sum_{i=1}^{7}({z}_{i}-\overline{z})({t}_{i}-\overline{t})}{\sum_{i=1}^{7}({t}_{i}-\overline{t})^{2}}$ |
| 1157.54 | 0.43 | 0.32 | 0.00012 |
附:对于一组数据(u1,v1),(u2,v2),…,(un,vn),其回归直线v=βu+α的斜率和截距的最小二乘估计分别为:β=$\frac{\sum_{i=1}^{n}({u}_{i}-\overline{u})({v}_{i}-\overline{v})}{\sum_{i=1}^{n}({u}_{i}-\overline{u})^{2}}$,α=$\overline{v}$-β$\overline{u}$.
(1)分别画出y关于t的散点图、z关于x的散点图,根据散点图判断哪一个模型更适宜作为回归方程类型?(给出判断即可,不必说明理由).
(2)根据表中数据,分别建立两个模型下建立y关于x的回归方程;并在两个模型下分别估计温度为30℃时的产卵数.(C1,C2,C3,C4与估计值均精确到小数点后两位)(参考数据:e4.65≈104.58,e4.85≈127.74,e5.05≈156.02)
(3)若模型①、②的相关指数计算分别为R12=0.82,R22=0.96,请根据相关指数判断哪个模型的拟合效果更好.

9.已知函数f(x)=xlnx-aex(e为自然对数的底数)有两个极值点,则实数a的取值范围是( )
| A. | $({0,\frac{1}{e}})$ | B. | (0,e) | C. | $({\frac{1}{e},e})$ | D. | (-∞,e) |
19.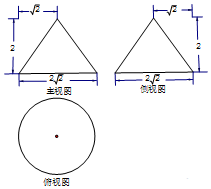 某工件的三视图如图所示,现将该工件通过切割,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工件的一个面内,则新工件的棱长为( )
某工件的三视图如图所示,现将该工件通过切割,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工件的一个面内,则新工件的棱长为( )
 某工件的三视图如图所示,现将该工件通过切割,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工件的一个面内,则新工件的棱长为( )
某工件的三视图如图所示,现将该工件通过切割,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工件的一个面内,则新工件的棱长为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | $2-\sqrt{2}$ |
6.已知定义[x]表示不超过的最大整数,如[2]=2,[2,2]=2,执行如图所示的程序框图,则输出S=( )

| A. | 1991 | B. | 2000 | C. | 2007 | D. | 2008 |
3.设集合A={x|0≤x≤2},B={x∈N|1≤x≤3},则A∩B=( )
| A. | {1,2} | B. | {1,2,3} | C. | {x|1≤x≤2} | D. | {x|0≤x≤3} |
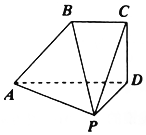 如图,五面体PABCD中,CD⊥平面PAD,ABCD为直角梯形,∠BCD=$\frac{π}{2}$,PD=BC=CD=$\frac{1}{2}$AD,AP⊥PD.
如图,五面体PABCD中,CD⊥平面PAD,ABCD为直角梯形,∠BCD=$\frac{π}{2}$,PD=BC=CD=$\frac{1}{2}$AD,AP⊥PD.