题目内容
15.已知函数f(x)=sinωx-$\sqrt{3}$cosωx(ω>0),若方程f(x)=-1在(0,π)上有且只有四个实数根,则实数ω的取值范围为( )| A. | ($\frac{13}{6}$,$\frac{7}{2}$] | B. | ($\frac{7}{2}$,$\frac{25}{6}$] | C. | ($\frac{25}{6}$,$\frac{11}{2}$] | D. | ($\frac{11}{2}$,$\frac{37}{6}$] |
分析 化简f(x)的解析式,作出f(x)的函数图象,利用三角函数的性质求出直线y=-1与y=f(x)在(0,+∞)上的交点坐标,则π介于第4和第5个交点横坐标之间.
解答 解:f(x)=2sin(ωx-$\frac{π}{3}$),
作出f(x)的函数图象如图所示: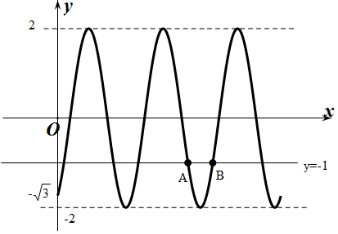
令2sin(ωx-$\frac{π}{3}$)=-1得ωx-$\frac{π}{3}$=-$\frac{π}{6}$+2kπ,或ωx-$\frac{π}{3}$=$\frac{7π}{6}$+2kπ,
∴x=$\frac{π}{6ω}$+$\frac{2kπ}{ω}$,或x=$\frac{3π}{2ω}$+$\frac{2kπ}{ω}$,k∈Z,
设直线y=-1与y=f(x)在(0,+∞)上从左到右的第4个交点为A,第5个交点为B,
则xA=$\frac{3π}{2ω}+$$\frac{2π}{ω}$,xB=$\frac{π}{6ω}+\frac{4π}{ω}$,
∵方程f(x)=-1在(0,π)上有且只有四个实数根,
∴xA<π≤xB,
即$\frac{3π}{2ω}+$$\frac{2π}{ω}$<π≤$\frac{π}{6ω}+\frac{4π}{ω}$,解得$\frac{7}{2}<ω≤\frac{25}{6}$.
故选B.
点评 本题考查了三角函数的恒等变换,三角函数的图象与性质,属于中档题.

练习册系列答案
相关题目
5.圆心在x轴上,半径为2,且过点(1,2)的圆的方程为( )
| A. | (x-1)2+y2=4 | B. | (x-2)2+y2=4 | C. | x2+(y-1)2=4 | D. | (x-1)2+(y-4)2=4 |
7.已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的半焦距为c(c>0),左焦点为F,右顶点为A,抛物线${y^2}=\frac{15}{8}(a+c)x$与椭圆交于M,N两点,若四边形AMFN是菱形,则椭圆的离心率是( )
| A. | $\frac{8}{15}$ | B. | $\frac{4}{15}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{2}$ |
 如图,矩形ABCD中,AB=2AD=2,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE,若M为线段A1C的中点,则在△ADE翻转过程中,对于下列说法:
如图,矩形ABCD中,AB=2AD=2,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE,若M为线段A1C的中点,则在△ADE翻转过程中,对于下列说法: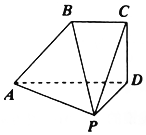 如图,五面体PABCD中,CD⊥平面PAD,ABCD为直角梯形,∠BCD=$\frac{π}{2}$,PD=BC=CD=$\frac{1}{2}$AD,AP⊥PD.
如图,五面体PABCD中,CD⊥平面PAD,ABCD为直角梯形,∠BCD=$\frac{π}{2}$,PD=BC=CD=$\frac{1}{2}$AD,AP⊥PD.