题目内容
已知P是△ABC所在平面内一点,
+
+2
=
,现将一粒黄豆随机撒在△ABC内,则黄豆落在△PBC内的概率是( )
| PB |
| PC |
| PA |
| 0 |
A.
| B.
| C.
| D.
|
以PB、PC为邻边作平行四边形PBDC,则
+
=
∵
+
+2
=
,
∴
+
=-2
,得
=-2
由此可得,P是△ABC边BC上的中线AO的中点,
点P到BC的距离等于A到BC的距离的
.
∴S△PBC=
S△ABC.
将一粒黄豆随机撒在△ABC内,黄豆落在△PBC内的概率为P=
=
故选C
| PB |
| PC |
| PD |
∵

| PB |
| PC |
| PA |
| 0 |
∴
| PB |
| PC |
| PA |
| PD |
| PA |
由此可得,P是△ABC边BC上的中线AO的中点,
点P到BC的距离等于A到BC的距离的
| 1 |
| 2 |
∴S△PBC=
| 1 |
| 2 |
将一粒黄豆随机撒在△ABC内,黄豆落在△PBC内的概率为P=
| S△PBC |
| S△ABC |
| 1 |
| 2 |
故选C

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中,已知
中,已知 ,
, ,
,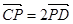 .
. 的值;
的值; ,求
,求 与
与 夹角的余弦值.
夹角的余弦值. ABCD的两条对角线AC与BD交于E,O是任意一点,
ABCD的两条对角线AC与BD交于E,O是任意一点, +
+ +
+ +
+ =4
=4

 ,
, .
.  ,求实数
,求实数 的值;
的值; 为直角三角形,求实数
为直角三角形,求实数 b=(3,1),c=(x,3),若(2a+b)∥c,则x= .
b=(3,1),c=(x,3),若(2a+b)∥c,则x= .