题目内容
(本小题满分12分)已知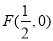 为抛物线
为抛物线 的焦点,点
的焦点,点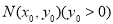
为其上一点,点M与点N关于x轴对称,直线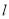 与抛物线交于异于M,N的A,B两点,且
与抛物线交于异于M,N的A,B两点,且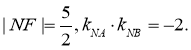
(1)求抛物线方程和N点坐标;
(2)判断直线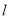 中,是否存在使得
中,是否存在使得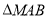 面积最小的直线
面积最小的直线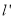 ,若存在,求出直线
,若存在,求出直线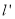 的方程和
的方程和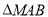 面积的最小值;若不存在,说明理由。
面积的最小值;若不存在,说明理由。
 ,
, ,
,
【解析】
试题分析:(1)有题意 ,
,  即
即 ,
, 得
得
所以抛物线方程为 ,
, 4分
4分
(2)由题意知直线的斜率不为0,设直线 的方程为
的方程为 (
( )
)
联立方程 得
得 ,
,
设两个交点

 6分
6分
 ,整理得
,整理得 8分
8分
此时 恒成立,
恒成立,
由此直线 的方程可化为
的方程可化为 从而直线
从而直线 过定点
过定点 9分
9分
因为 ,所以
,所以 所在直线平行
所在直线平行 轴
轴
三角形 面积
面积 11分
11分
所以当 时
时 有最小值为
有最小值为 ,此时直线
,此时直线 的方程为
的方程为 12分
12分
考点:本题考查直线与抛物线的位置关系

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的前
的前 项和为
项和为 ,若
,若 ,则
,则 等于( )
等于( ) ,则“
,则“ ”是“
”是“ ”的( )
”的( ) 的焦点,P为C上一点,若
的焦点,P为C上一点,若 ,则
,则 POF的面积为( )
POF的面积为( ) B.
B. C.2 D.3
C.2 D.3 ,则“a=±1”是“
,则“a=±1”是“ i为纯虚数”的( )
i为纯虚数”的( ) 的鸡蛋(视为球体)放在其上(如图),则鸡蛋中心(球心)与蛋托底面的距离为 .
的鸡蛋(视为球体)放在其上(如图),则鸡蛋中心(球心)与蛋托底面的距离为 .
 在
在 内有极小值,则实数
内有极小值,则实数 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
 个等式为 .
个等式为 .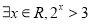 ”的否定是“
”的否定是“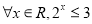 ”;
”;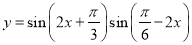 的最小正周期是
的最小正周期是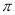 ;
; 在
在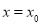 处有极值,则
处有极值,则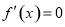 ”的否命题是真命题;
”的否命题是真命题; 上的奇函数,
上的奇函数,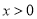 时的解析式是
时的解析式是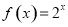 ,
,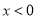 时的解析式为
时的解析式为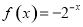 .
.