题目内容
某工厂生产某种产品,每日的成本C(单位:元)与日产量x(单位:t)满足函数关系式C=10 000+20x,每日的销售额R(单位:元)与日产量x的函数关系式为R=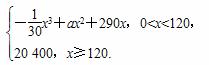
已知每日的利润y=R-C,且当x=30时,y=-100.
(1)求a的值;
(2)当日产量为多少吨时,每日的利润可以达到最大,并求出最大值.
(1)∵当x=30时,y=-100,
∴-100=- ×303+a×302+270×30-10 000,
×303+a×302+270×30-10 000,
∴a=3.
(2)当0<x<120时,y=- x3+3x2+270x-10 000.
x3+3x2+270x-10 000.
令y′=- x2+6x+270=0,
x2+6x+270=0,
可得:x1=90,x2=-30(舍去),
所以当x∈(0,90)时,原函数是增函数,当x∈(90,120)时,原函数是减函数.
∴当x=90时,y取得极大值14 300.
当x≥120时,y=10 400-20x≤8 000.
所以当日产量为90t时,每日的利润可以达到最大值14 300元.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
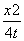 +
+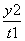 =1表示曲线C,给出以下命题:
=1表示曲线C,给出以下命题: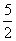 .
.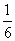 ,-
,-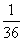 )
)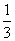 ,-
,-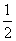 )或(-
)或(-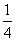 ,
, )
) 则f(f(3))=( )
则f(f(3))=( ) B.3
B.3 D.
D.
 的定义域是________.
的定义域是________.