题目内容

12．如图，在正方形ABCD-A1B1C1D1中，
（1）求异面直线AD1与BD所成角的大小；
（2）求二面角D1-CB-D的大小．

分析 （1）由AD1∥BC1，得∠DBC1是异面直线AD1与BD所成角，由此能求出异面直线AD1与BD所成角的大小．
（2）由正方体性质得D1C⊥BC，DC⊥BC，从而∠DCD1是二面角D1-CB-D的平面角，由此能求出二面角D1-CB-D的大小．

解答 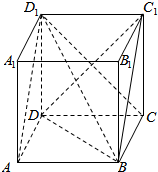解：（1）∵AD1∥BC1，∴∠DBC1是异面直线AD1与BD所成角，
连结BD，DC1，则BD=DC1=BC1，
∴∠DBC1=60°，
∴异面直线AD1与BD所成角的大小为60°．
（2）∵BC⊥平面DCC1D1，D1C?平面DCC1D1，DC?平面DCC1D1，
∴D1C⊥BC，DC⊥BC，
∴∠DCD1是二面角D1-CB-D的平面角，
∵D1D=DC，D1D⊥DC，∴∠DCD1=45°，
∴二面角D1-CB-D的大小为45°．

点评 本题考查异面直线所成角的大小的求法，考查二面角的大小的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．

练习册系列答案
相关题目
2．已知$\frac{z-1}{z+1}$为纯虚数，且（z+1）（$\overline{z}$+1）=|z|2，求复数z．
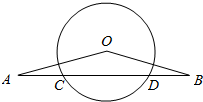3．已知：如图△OAB为等腰三角形，底边AB角⊙O于点C，D，求证：AC=BD．
20．设数列{an}的前n项和为Sn，a1=1，Sn+1=4an+2．求证：{an+1-2an}为等比数列．
7．如图，已知在长方体ABCD-A1B1C1D1中，AB=2，AA1=1，直线BD与平面AA1B1B所成的角为30°，AE垂直BD于点E，F为A1B1的中点．
（1）求异面直线AE与BF所成角的余弦值；
（2）求平面BDF与平面AA1B所成二面角（锐角）的余弦值．
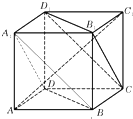17．如图正方体ABCD-A1B1C1D1中，下列结论中正确的序号是①③．
①平面A1BD∥平面CB1D1
②AC1与CD1相交
③AC1⊥平面CB1D1   
④异面直线AD与CB1所成角为60°．
4．若函数y=sin（$\frac{π}{3}$-2x），则函数在[-π，0]上的单调递减区间是[-$\frac{π}{12}$，0]和，[-π，-$\frac{7π}{12}$]．
1．f（x）=$\frac{x}{1-\sqrt{1-x}}$的定义域（　　）
A．（-∞，1]B．（-∞，0）∪（0，1）C．（-∞，0）∪（0，1]D．[1，+∞）
2．已知非零向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$满足|$\overrightarrow{a}$|≥1，|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|=2，（$\overrightarrow{c}$-$\overrightarrow{a}$）•（$\overrightarrow{c}$-$\overrightarrow{b}$）=3，则|$\overrightarrow{b}$|的最大值是$\sqrt{3}$；|$\overrightarrow{c}$|的取值范围是[1，3]．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网