题目内容
20.设数列{an}的前n项和为Sn,a1=1,Sn+1=4an+2.求证:{an+1-2an}为等比数列.分析 Sn+1=4an+2,a1=1,当n=1时,1+a2=4×1+2,解得a2;当n≥2时,an+1=Sn+1-Sn,变形为an+1-2an=2(an-2an-1),即可证明;
解答 证明:∵Sn+1=4an+2,a1=1,
∴当n=1时,1+a2=4×1+2,解得a2=5;
当n≥2时,an+1=Sn+1-Sn=4an+2-(4an-1+2),
化为an+1=4an-4an-1,
∴an+1-2an=2(an-2an-1),
∴数列:{an+1-2an}是等比数列,首项为a2-2a1=3,公比为2.
点评 本题主要考查等比数列的判断和证明,根据数列的递推关系利用构造法是解决本题的关键.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
 如图,在正方形ABCD-A1B1C1D1中,
如图,在正方形ABCD-A1B1C1D1中,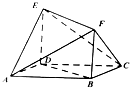 如图所示的多面体中,ABCD是菱形,BDEF是矩形,ED⊥面ABCD,∠BAD=$\frac{π}{3}$.
如图所示的多面体中,ABCD是菱形,BDEF是矩形,ED⊥面ABCD,∠BAD=$\frac{π}{3}$.