题目内容
6.“中国式过马路”存在很大的交通安全隐患.某调查机构为了解路人对“中国式过马路”的态度是否与性别有关,从马路旁随机抽取20名路人进行了问卷调查,得到了如下列联表:| 男性 | 女性 | 合计 | |
| 反感 | 8 | 2 | 10 |
| 不反感 | 6 | 4 | 10 |
| 合计 | 14 | 6 | 20 |
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
(Ⅱ)若从这20人中的女性路人中随机抽取2人参加一活动,求至少有1人反感“中国式过马路”的概率.
分析 (Ⅰ)在这20人中随机抽取1人抽到反感“中国式过马路”的路人的概率是$\frac{1}{2}$,填好表格;根据所给的公式,代入数据求出临界值,把求得的结果同临界值表进行比较,看出有多大的把握说明反感“中国式过马路”与性别是否有关.
(Ⅱ)求出基本事件的个数,即可求至少有1人反感“中国式过马路”的概率.
解答 解:列联表:
| 男性 | 女性 | 合计 | |
| 反感 | 8 | 2 | 10 |
| 不反感 | 6 | 4 | 10 |
| 合计 | 14 | 6 | 20 |
∴没有充足的理由认为反感“中国式过马路”与性别有关;
(Ⅱ)若从6名女性路人中随机抽取2人参加一活动,有C62=15种;至少有1人反感“中国式过马路”有15-C42=9种,
∴至少有1人反感“中国式过马路”的概率是$\frac{9}{15}$=$\frac{3}{5}$.
点评 本题考查了独立性检验,考查概率的计算,考查学生分析解决问题的能力,比较基础.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
14.已知向量$\overrightarrow{AB}$=(3,1),$\overrightarrow{AC}$=(2,4),则向量$\overrightarrow{BC}$=( )
| A. | (5,5) | B. | (6,4) | C. | (-1,3) | D. | (1,-3) |
11.运用秦九韶算法求n次多项式的值时,考虑到可能有的系数为0,那么最多要进行( )次乘法运算.
| A. | n | B. | n-1 | C. | n+1 | D. | 以上都不对 |
18.设{an}是等比数列,下列结论中正确的是( )
| A. | 若a1+a2>0,则a2+a3>0 | B. | 若a1+a3<0,则a1+a2<0 | ||
| C. | 若0<a1<a2,则2a2<a1+a3 | D. | 若a1<0,则(a2-a1)(a2-a3)>0 |
15.已知等比数列{an}的前n项和为Sn,则下列不可能成立的( )
| A. | a2016(S2016-S2015)=0 | B. | a2016(S2016-S2014)=0 | ||
| C. | (a2016-a2013)(S2016-S2013)=0 | D. | (a2016-a2012)(S2016-S2012)=0 |
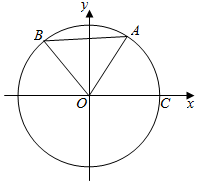 如图,在平面直角坐标系xOy中,点A,B均在单位圆上,已知点A在第一象限,横坐标为$\frac{\sqrt{3}}{3}$,点B在第二象限.若△AOB为正三角形,则点B的坐标为B($\frac{\sqrt{3}-3\sqrt{2}}{6}$,$\frac{3+\sqrt{6}}{6}$).
如图,在平面直角坐标系xOy中,点A,B均在单位圆上,已知点A在第一象限,横坐标为$\frac{\sqrt{3}}{3}$,点B在第二象限.若△AOB为正三角形,则点B的坐标为B($\frac{\sqrt{3}-3\sqrt{2}}{6}$,$\frac{3+\sqrt{6}}{6}$).