题目内容
15．已知等比数列{an}的前n项和为Sn，则下列不可能成立的（ ）| A． | a2016（S2016-S2015）=0 | B． | a2016（S2016-S2014）=0 | ||
| C． | （a2016-a2013）（S2016-S2013）=0 | D． | （a2016-a2012）（S2016-S2012）=0 |
分析 根据等比数列中的项不等于0的性质进行判断．
解答 解：∵{an}是等比数列，∴a2016=S2016-S2015≠0，∴a2016（S2016-S2015）≠0；
当{an}的公比为-1时，S2016-S2014=a2015+a2016=0，∴a2016（S2016-S2014）=0；
当{an}的公比为1时，a2016=a2013=a2012，∴（a2016-a2013）（S2016-S2013）=0；（a2016-a2012）（S2016-S2012）=0．
故选A．
点评 本题考查了等比数列的性质，属于基础题．
练习册系列答案
相关题目
6．“中国式过马路”存在很大的交通安全隐患．某调查机构为了解路人对“中国式过马路”的态度是否与性别有关，从马路旁随机抽取20名路人进行了问卷调查，得到了如下列联表：
已知在这20人中随机抽取1人抽到反感“中国式过马路”的路人的概率是$\frac{1}{2}$．
附：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$
（Ⅰ）请将上面的列联表补充完整（直接填写结果，不需要写求解过程），并据此资料分析反感“中国式过马路”与性别是否有关？
（Ⅱ）若从这20人中的女性路人中随机抽取2人参加一活动，求至少有1人反感“中国式过马路”的概率．
| 男性 | 女性 | 合计 | |
| 反感 | 8 | 2 | 10 |
| 不反感 | 6 | 4 | 10 |
| 合计 | 14 | 6 | 20 |
附：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$
| P（K2≥k） | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
（Ⅱ）若从这20人中的女性路人中随机抽取2人参加一活动，求至少有1人反感“中国式过马路”的概率．
10．已知集合A={1，2，3}，则“a=3”是“a∈A“的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既充分也不必要条件 |
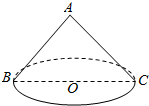如图，已知圆锥的轴截面是腰长为$\sqrt{2}$的等腰直角三角形．试求：