题目内容
学习曲线是1936年美国康乃尔大学T.P.Wright博士在飞机制造过程中,通过对大量有关资料、案例的观察、分析、研究,首次发现并提出来的.已知某类学习任务的学习曲线为:f(t)=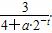 ·100%(其中f(t)为掌握该任务的程度,t为学习时间),且这类学习任务中的某项任务满足f(2)=60%.
·100%(其中f(t)为掌握该任务的程度,t为学习时间),且这类学习任务中的某项任务满足f(2)=60%.
(1)求f(t)的表达式,计算f(0)并说明f(0)的含义;
(2)已知2x>xln2对任意x>0恒成立,现定义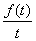 为该类学习任务在t时刻的学习效率指数,研究表明,当学习时间t∈(1,2)时,学习效率最佳,当学习效率最佳时,求学习效率指数相应的取值范围.
为该类学习任务在t时刻的学习效率指数,研究表明,当学习时间t∈(1,2)时,学习效率最佳,当学习效率最佳时,求学习效率指数相应的取值范围.
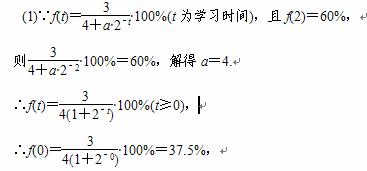 f(0)表示某项学习任务在开始学习时已掌握的程度为37.5%.
f(0)表示某项学习任务在开始学习时已掌握的程度为37.5%.
(2)令学习效率指数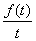 =y,
=y,
则y=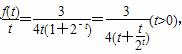 现研究函数g(t)=t+
现研究函数g(t)=t+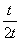 的单调性,
的单调性,
由于g′(t)=1+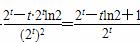 (t>0),
(t>0),
又已知2x>xln2对任意x>0恒成立,即2t-tln2>0,则g′(t)>0恒成立,
∴g(t)在(0,+∞)上为增函数,且g(t)为正数.
∴y=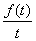 =
=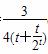 (t>0)在(0,+∞)上为减函数,
(t>0)在(0,+∞)上为减函数,
而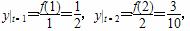
即y=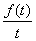 ∈(
∈(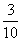 ,
,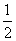 ),
),
故所求学习效率指数的取值范围是(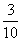 ,
,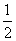 ).
).

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目


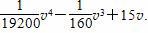 .
. f ′(x)dx=0的实数a有________个.( )
f ′(x)dx=0的实数a有________个.( ) +x2)3的展开式中的常数项为a,则直线y=ax与直线y=x2围成图形的面积为( )
+x2)3的展开式中的常数项为a,则直线y=ax与直线y=x2围成图形的面积为( ) B.9
B.9 D.
D.
 ,则
,则 ( )
( ) B.
B. C.
C. D.
D.