题目内容
1.已知正项等差数列{an}和正项等比数列{bn}满足,a5=b5,则下列关系正确的是( )| A. | a1+a9≥b1+b9 | B. | a1+a9≤b1+b9 | C. | a1+a9>b1+b9 | D. | a1+a9<b1+b9 |
分析 根据等差中项和等比中项以及基本不等式即可判断
解答 解:∵数列{an}是等差数列
∴a5=$\frac{1}{2}$(a1+a9),
∵数列{bn}是等比数列
∴b5=$\sqrt{{b}_{1}{b}_{9}}$,
∴b1+b9≥2$\sqrt{{b}_{1}{b}_{9}}$=2b5=2a5=a1+a9,
故选:D.
点评 本题主要考查了等差数列和等比数列的性质.属基础题.

练习册系列答案
相关题目
11.已知△ABC的面积为30,且cosA=$\frac{12}{13}$,则$\overrightarrow{AB}$$•\overrightarrow{AC}$等于( )
| A. | 72 | B. | 144 | C. | 150 | D. | 300 |
6.若向量$\overrightarrow a=(1,1)$,$\overrightarrow b=(-1,2)$,$\overrightarrow c=(1,-1)$,则$\overrightarrow c$等于( )
| A. | $-\frac{1}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b$ | B. | $\frac{2}{3}\overrightarrow a-\frac{1}{3}\overrightarrow b$ | C. | $\frac{1}{3}\overrightarrow a-\frac{2}{3}\overrightarrow b$ | D. | $-\frac{2}{3}\overrightarrow a+\frac{1}{3}\overrightarrow b$ |
13.已知A={x|x2-3x+2≤0},B={-2,-1,0,1,2},则A∩B=( )
| A. | {-1,0} | B. | {0,1} | C. | {1,2} | D. | ∅ |
11.已知函数f(x)=2x-e2x(e为自然对数的底数),g(x)=mx+1,(m∈R),若对于任意的x1∈[-1,1],总存在x0∈[-1,1],使得g(x0)=f(x1)成立,则实数m的取值范围为( )
| A. | (-∞,1-e2]∪[e2-1,+∞) | B. | [1-e2,e2-1] | ||
| C. | (-∞,e-2-1]∪[1-e-2,+∞) | D. | [e-2-1,1-e-2] |
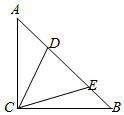 如图,等腰直角三角形区域ABC中,∠ACB=90°,BC=AC=1百米.现准备划出一块三角形区域CDE,其中D,E均在斜边AB上,且∠DCE=45°.记三角形CDE的面积为S.
如图,等腰直角三角形区域ABC中,∠ACB=90°,BC=AC=1百米.现准备划出一块三角形区域CDE,其中D,E均在斜边AB上,且∠DCE=45°.记三角形CDE的面积为S.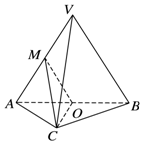 如图,在三棱锥VABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC,O,M分别为AB,VA的中点.
如图,在三棱锥VABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC,O,M分别为AB,VA的中点.