题目内容
cosθ-sinθ=
,则sin2θ=( )
| ||
| 3 |
A、-
| ||
B、
| ||
C、
| ||
D、-
|
考点:二倍角的正弦
专题:三角函数的求值
分析:把已知式子平方,由三角函数公式可得.
解答:
解:∵cosθ-sinθ=
,∴(cosθ-sinθ)2=
,
∴1-2sinθcosθ=
,∴sin2θ=2sinθcosθ=
,
故选:B
| ||
| 3 |
| 2 |
| 9 |
∴1-2sinθcosθ=
| 2 |
| 9 |
| 7 |
| 9 |
故选:B
点评:本题考查二倍角的正弦公式,把已知式子平方是解决问题的关键,属基础题.

练习册系列答案
相关题目
已知向量|
|=2,|
|=1,且
,
夹角为60°,则向量
+
与
-
的夹角的余弦的值是( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、3 | ||||
B、
| ||||
C、
| ||||
D、
|
复数z=i2(1-i)(其中i为虚数单位)的值是( )
| A、1-i | B、1+i |
| C、-1-i | D、-1+i |
不等式
>1的解集为( )
| 2 |
| x-1 |
| A、{x|x>3} |
| B、{x|1<x<3} |
| C、{x|x<3} |
| D、{x|x<3或x>1} |
已知复数z=a2-1+(a+1)i(a∈R)为纯虚数,则
为( )
. |
| z |
| A、0 | B、2i |
| C、-2i | D、-1-2i |
若x>y>1,0<a<1,那么下列各式中正确的是( )
| A、x-a>y-a |
| B、logax>logay |
| C、ax<ay |
| D、ax>ay |
设全集U=R,A={x|x(x-2)<0},B={x|y=ln(1-x)<0},则图中阴影部分表示的集合为( )
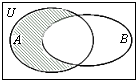

| A、{x|0<x≤1} |
| B、{x|1≤x<2} |
| C、{x|x≥1} |
| D、{x|x≤1} |
函数y=(
)x+2+1(a>0,a≠1)图象必经过点( )
| 1 |
| a |
| A、(-1,1) |
| B、(-1,2) |
| C、(-2,1) |
| D、(-2,2) |