题目内容
4.设抛物线y=mx2(m≠0)的准线与直线y=1的距离为3,求抛物线的标准方程.分析 根据抛物线y=mx2写出它的准线方程y=-$\frac{1}{4m}$,再根据准线与直线y=1的距离为3,对m的正负进行讨论,即可求得m的值,进而求得抛物线的方程.
解答 解:当m>0时,准线方程为y=-$\frac{1}{4m}$,1+$\frac{1}{4m}$=3,
∴m=$\frac{1}{8}$,
此时抛物线方程为y=$\frac{1}{8}$x2;
当m<0时,准线方程为y=-$\frac{1}{4m}$,-$\frac{1}{4m}$-1=3,
∴m=-$\frac{1}{16}$,
此时抛物线方程为y=-$\frac{1}{16}$x2;
∴所求抛物线的标准方程为x2=8y或x2=-16y.
故答案为:x2=8y或x2=-16y.
点评 此题是个中档题.考查抛物线的定义和简单的几何性质,以及待定系数法求抛物线的标准方程.体现了数形结合的思想,特别是解析几何,一定注意对几何图形的研究,以便简化计算.

练习册系列答案
相关题目
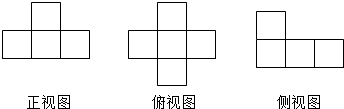
14.如图(1)、(2)、(3)、(4)为四个几何体的三视图,根据三视图可以判断这四个几何体依次分别为
( )
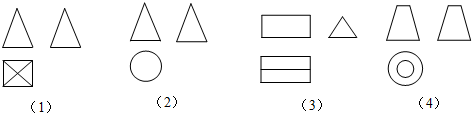
( )

| A. | 四棱台、圆锥、三棱柱、圆台 | B. | 三棱锥、圆锥、三棱台、圆台 | ||
| C. | 四棱锥、圆锥、三棱柱、圆台 | D. | 三棱柱、三棱台、圆锥、圆台 |
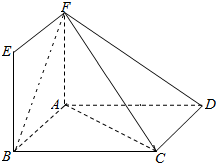 在如图所示的几何体中,四边形ABCD为平行四边形,平面ABEF⊥平面ABCD,∠ACD=90°,AB=2,AD=4,ABEF为正方形,平面ABEF⊥平面ABCD,AN⊥CF,垂足为N.
在如图所示的几何体中,四边形ABCD为平行四边形,平面ABEF⊥平面ABCD,∠ACD=90°,AB=2,AD=4,ABEF为正方形,平面ABEF⊥平面ABCD,AN⊥CF,垂足为N.