题目内容
13.公差为d的等差数列{an}的前n项和为Sn(n∈N*),已知S5=a${\;}_{3}^{2}$,且a2,a5,a14成等比数列.(1)求{an}的通项公式;
(2)当d≠0时,数列{$\frac{1}{{S}_{n}+2n}$}的前n项和为Tn,试比较Tn与$\frac{3}{4}$的大小.
分析 (1)通过等差中项的性质及S5=a${\;}_{3}^{2}$可知a3=5,结合a2,a3,a14成等比数列可知d=0或d=2,进而计算可得结论;
(2)通过(1)及d≠0可知an=2n-1,进而裂项可知$\frac{1}{{S}_{n}+2n}$=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+2}$),并项相加即得结论.
解答 解:(1)依题意,$\left\{\begin{array}{l}{5{a}_{3}={{a}_{3}}^{2}}\\{({a}_{3}+2d)^{2}=({a}_{3}-d)({a}_{3}+11d)}\end{array}\right.$,$\underset{\stackrel{①}{\;}}{②}$
由①解得:a3=0(舍)或a3=5,
将a3=5代入②得d=0或d=2,
当d=0时an=5,当d=2时an=2n-1;
(2)由(1)及d≠0可知an=2n-1,
∵$\frac{1}{{S}_{n}+2n}$=$\frac{1}{\frac{n(1+2n-1)}{2}+2n}$=$\frac{1}{n(n+2)}$=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+2}$),
∴Tn=$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{2}$-$\frac{1}{4}$+…+$\frac{1}{n-1}$-$\frac{1}{n+1}$+$\frac{1}{n}$-$\frac{1}{n+2}$)
=$\frac{1}{2}$(1+$\frac{1}{2}$-$\frac{1}{n+1}$-$\frac{1}{n+2}$)
=$\frac{3}{4}$-$\frac{1}{2}$($\frac{1}{n+1}$+$\frac{1}{n+2}$)
<$\frac{3}{4}$.
点评 本题考查数列的通项及前n项和,考查运算求解能力,考查裂项相消法,注意解题方法的积累,属于中档题.


| A. | $\frac{10}{3}$ | B. | 4 | C. | 6 | D. | 10 |
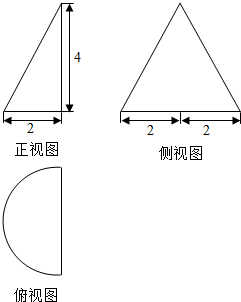
| A. | $\frac{4}{3}π$ | B. | $\frac{8}{3}π$ | C. | $\frac{16}{3}π$ | D. | $\frac{32}{3}π$ |
| 参加纪念活动的环节数 | 0 | 1 | 2 | 3 |
| 概率 | $\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{6}$ | $\frac{1}{6}$ |
(Ⅱ)某医疗部门决定从这些抗战老兵中(其中参加纪念活动的环节数为3的抗战老兵数大于等于3)随机抽取3名进行体检,设随机抽取的这3名抗战老兵中参加三个环节的有ξ名,求ξ的分布列和数学期望.