题目内容
集合M={x|-2<x<3},N={x|2x+1≥1},则(∁RM)∩N=( )
| A、(3,+∞) |
| B、[3,+∞) |
| C、[-1,3) |
| D、(-1,3) |
考点:交、并、补集的混合运算
专题:集合
分析:求出N中不等式的解集确定出N,根据全集R与M求出M的补集,找出M补集与N的交集即可.
解答:
解:由N中的不等式变形得:2x+1≥1=20,即x+1≥0,
解得:x≥-1,即N=[-1,+∞);
∵M=(-2,3),
∴∁RM=(-∞,-2]∪[3,+∞),
则(∁RM)∩N=[3,+∞).
故选:B.
解得:x≥-1,即N=[-1,+∞);
∵M=(-2,3),
∴∁RM=(-∞,-2]∪[3,+∞),
则(∁RM)∩N=[3,+∞).
故选:B.
点评:此题考查了交、并、补集的混合运算,熟练掌握各自的定义是解本题的关键.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
设e1,e2是焦点在x轴上,中心在原点且有公共交点F1,F2的椭圆和双曲线的离心率,O为坐标原点,P是双曲线的一个公共点,且满足2|OP|=|F1F2|,则
的值为( )
|
| A、2 | ||||
B、
| ||||
C、
| ||||
| D、1 |
点(0,5)到直线2x-y=0的距离是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在区间[-3,3]上任取一个数a,则圆C1:x2+y2+4x-5=0与圆C2:(x-a)2+y2=1有公共点的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知向量
=(2,3),
=(k,-1),
⊥
,则k=( )
| a |
| b |
| a |
| b |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
已知复数
=b+i(a,b∈R,i为虚数单位),则a-2b=( )
| a-2i |
| i |
| A、1 | B、2 | C、3 | D、4 |
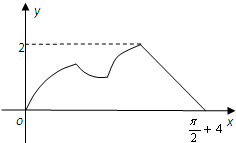
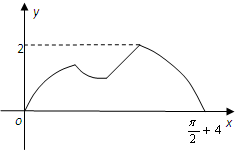
 已知函数f(x)=2sin(ωx+φ)(其中x∈R,ω>0,-π<φ<π)的部分图象如图所示.如果对函数g(x)的图象进行如下变化:横坐标扩大为原来的2倍,纵坐标不变,也可得到f(x)函数的图象,则函数g(x)的解析式是
已知函数f(x)=2sin(ωx+φ)(其中x∈R,ω>0,-π<φ<π)的部分图象如图所示.如果对函数g(x)的图象进行如下变化:横坐标扩大为原来的2倍,纵坐标不变,也可得到f(x)函数的图象,则函数g(x)的解析式是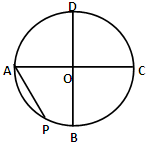 如图,圆O的半径为1,AC⊥BD,动点P从点A出发,沿圆弧
如图,圆O的半径为1,AC⊥BD,动点P从点A出发,沿圆弧