题目内容
3.在下列四个正方体中,能得出AB⊥CD的是( )| A. |  | B. |  | C. |  | D. |  |
分析 在A中,推导出线面垂直,从而得到AB⊥CD;在B中,AB与CD成60°角;在C中,AB与CD成45°角;在D中,AB与CD所成角的正切值为$\sqrt{2}$.
解答 解:在A中, CD⊥BE,CD⊥AE,BE∩AE=E,
CD⊥BE,CD⊥AE,BE∩AE=E,
∴CD⊥平面ABE,又AB?平面ABE,∴AB⊥CD,故A正确;
在B中,AB与CD成60°角,故B错误;
在C中,AB与CD成45°角,故C错误;
在D中,AB与CD所成角的正切值为$\sqrt{2}$,故D错误.
故选:A.
点评 本题考查两异面直线垂直的判断,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力,考查化归与转化思想、数形结合思想,是中档题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
14. 阅读如图所示的程序框图,程序结束时,输出S的值为( )
阅读如图所示的程序框图,程序结束时,输出S的值为( )
 阅读如图所示的程序框图,程序结束时,输出S的值为( )
阅读如图所示的程序框图,程序结束时,输出S的值为( )| A. | 6 | B. | 21 | C. | 58 | D. | 141 |
18.附属z满足z=$\frac{3-i}{i}$,则在复平面内,复数z对应的点位于( )
| A. | 第乙象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
12.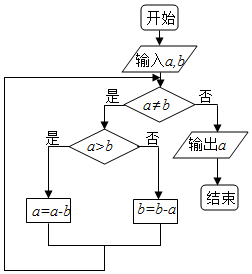 《九章算术》是我国古代数学名著,汇集古人智慧,其中的“更相减损术”更是有着深刻的应用.如图所示程序框图的算法思想即来源于此,若输入的a=2016,输出的a=21,则输入的b可能为( )
《九章算术》是我国古代数学名著,汇集古人智慧,其中的“更相减损术”更是有着深刻的应用.如图所示程序框图的算法思想即来源于此,若输入的a=2016,输出的a=21,则输入的b可能为( )
 《九章算术》是我国古代数学名著,汇集古人智慧,其中的“更相减损术”更是有着深刻的应用.如图所示程序框图的算法思想即来源于此,若输入的a=2016,输出的a=21,则输入的b可能为( )
《九章算术》是我国古代数学名著,汇集古人智慧,其中的“更相减损术”更是有着深刻的应用.如图所示程序框图的算法思想即来源于此,若输入的a=2016,输出的a=21,则输入的b可能为( )| A. | 288 | B. | 294 | C. | 378 | D. | 399 |
10.某公司10位员工的月工资(单位:元)为x1,x2,…x10,其均值和方差分别为$\overline{x}$和s2,若从下月起每位员工的月工次增加200元,则这10位员工下月工资的均值和方差分别为( )
| A. | $\overline{x}$,s2 | B. | $\overline{x}$+200,s2 | C. | $\overline{x}$,2002s2 | D. | $\overline{x}$+200,s2+2002 |