题目内容
函数y=cosx（x∈[0，2π]）的单调递减区间是
[0，π]
[0，π]
．分析：先求出y=cosx的单调减区间，然后与[0，2π]取交集即可．
解答：解：y=cosx的单调减区间为：[2kπ，2kπ+π]（k∈Z），
又x∈[0，2π]，
所以所求单调减区间为x∈[0，π]，
故答案为：[0，π]．
又x∈[0，2π]，
所以所求单调减区间为x∈[0，π]，
故答案为：[0，π]．
点评：本题考查余弦函数的单调性及单调区间的求法，注意单调区间为定义域的子集．
练习册系列答案
黄冈冠军课课练系列答案
相关题目
函数y=cosx（x∈R）的图象向左平移
个单位后，得到函数y=g（x）的图象，则g（x）的解析式为（ ）
| π |
| 2 |
| A、-sinx | B、sinx |
| C、-cosx | D、cosx |
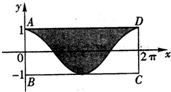如图所示，墙上挂有一长为2π，宽为2的矩形木板ABCD，它的阴影部分是由函数y=cosx，x∈[0，2π]的图象和直线y=1围成的图形．某人向此板投镖，假设每次都能投中木板，且击中木板上每个点的可能性都一样，则他击中阴影部分的概率是
在函数y=cosx，x∈[
在函数