题目内容

已知数列{an}满足a1=1，an+1=
(3n+3)an+4n+6
n
（n∈N*）．
（Ⅰ）证明：数列{
an
n
+
2
n
}是等比数列；
（Ⅱ）令bn=
3n-1
an+2
，数列{bn}的前n项和为Sn．
①证明：bn+1+bn+2+…+b2n＜
4
5

②证明：当n≥2时，Sn2＞2（
S2
2
+
S3
3
+…+
Sn
n
）
考点：数列的求和,等比关系的确定,数列与不等式的综合
专题：等差数列与等比数列
分析：（Ⅰ）由已知得
an+1
n+1
=3×
an
n
+
4n+6
n(n+1)
，由此能推导出数列{
an
n
+
2
n
}是等比数列是以1为首项，3为公比的等比数列．
（Ⅱ）（ⅰ）由
an
n
+
2
n
=3n-1，得an=n•3n-1-2，从而bn=
1
n
，原不等式即为：
1
n+1
+
1
n+2
+…+
1
2n
＜
4
5
，先用数学归纳法证明不等式当n≥2时，
1
n+1
+
1
n+2
+…+
1
2n
＜
4
5
-
1
2n+1
，由此能证明bn+1+bn+2+…+b2n＜
4
5
．
（ⅱ）由Sn=1+
1
2
+
1
3
+…+
1
n
，得当n≥2，Sn2-Sn-12=2•
Sn
n
-
1
n2
，从而利用累加法得Sn2-1=2(
S2
2
+
S3
3
+…+
Sn
n
)-(
1
22
+
1
32
+…+
1
n2
)，进而得到Sn2＞2(
S2
2
+
S3
3
+…+
Sn
n
)+
1
n
＞2（
S2
2
+
S3
3
+…+
Sn
n
），由此能证明当n≥2时，Sn2＞2（
S2
2
+
S3
3
+…+
Sn
n
）．
解答： （Ⅰ）证明：∵数列{an}满足a1=1，an+1=
(3n+3)an+4n+6
n
（n∈N*），
∴nan=3（n+1）an+4n+6，
两边同除n（n+1）得，
an+1
n+1
=3×
an
n
+
4n+6
n(n+1)
，
即
an+1
n+1
=3×
an
n
+
6
n
-
2
n+1
，
也即
an+1
n+1
+
2
n+1
=3×(
an
n
+
2
n
)，
又a1=-1，∴
a1
1
+
2
1
=1≠0，
∴数列{
an
n
+
2
n
}是等比数列是以1为首项，3为公比的等比数列．

（Ⅱ）（ⅰ）证明：由（Ⅰ）得，
an
n
+
2
n
=3n-1，∴an=n•3n-1-2，
∴bn=
1
n
，
原不等式即为：
1
n+1
+
1
n+2
+…+
1
2n
＜
4
5
，
先用数学归纳法证明不等式：
当n≥2时，
1
n+1
+
1
n+2
+…+
1
2n
＜
4
5
-
1
2n+1
，
证明过程如下：
当n=2时，左边=
1
3
+
1
4
=
7
12
=
35
60
＜
36
60
=
4
5
-
1
2×2+1
，不等式成立
假设n=k时，不等式成立，即
1
k+1
+
1
k+2
+…+
1
2k
＜
4
5
-
1
2k+1
，
则n=k+1时，左边=
1
k+2
+
1
k+3
+…+
1
2k
+
1
2k+1
+
1
2k+2

＜
4
5
-
1
2k+1
-
1
2k+1
-
1
k+1
+
1
2k+1
+
1
2k+2

=
4
5
-
1
2k+2
＜
4
5
-
1
2(k+1)+1
，
∴当n=k+1时，不等式也成立．
因此，当n≥2时，
1
n+1
+
1
n+2
+…+
1
2n
＜
4
5
-
1
2n+1
，
当n≥2时，
4
5
-
1
2n+1
＜
4
5
，
∴当n≥2时，
1
n+1
+
1
n+2
+…+
1
2n
＜
4
5
，
又当n=1时，左边=
1
2
＜
4
5
，不等式成立
故bn+1+bn+2+…+b2n＜
4
5
．
（ⅱ）证明：由（i）得，Sn=1+
1
2
+
1
3
+…+
1
n
，
当n≥2，Sn2-Sn-12=（1+
1
2
+…+
1
n-1
+
1
n
）2-（1+
1
2
+…+
1
n-1
）2
=
1
n
(2Sn-
1
n
)
=2•
Sn
n
-
1
n2
，
Sn-12-Sn-22=2•
Sn-1
n-1
-
1
(n-1)2
，
…
S22-S12=2•
S2
2
-
1
22
，
将上面式子累加得，Sn2-1=2(
S2
2
+
S3
3
+…+
Sn
n
)-(
1
22
+
1
32
+…+
1
n2
)，
又
1
22
+
1
32
+…+
1
n2
＜
1
1×2
+
1
2×3
+…+
1
(n-1)×n

=1-
1
2
+
1
2
-
1
3
+…+
1
n-1
-
1
n

=1-
1
n
，
∴Sn2-1＞2(
S2
2
+
S3
3
+…+
Sn
n
)-(1-
1
n
)，
即Sn2＞2(
S2
2
+
S3
3
+…+
Sn
n
)+
1
n
＞2（
S2
2
+
S3
3
+…+
Sn
n
），
∴当n≥2时，Sn2＞2（
S2
2
+
S3
3
+…+
Sn
n
）．
点评：本题考查等比数列的证明，考查不等式的证明，解题时要认真审题，注意构造法、累加法、裂项求和法、数学归纳法、放缩法的合理运用，综合性强，难度大，对数学思维能力的要求较高．
练习册系列答案
相关题目
为了开展全民健身运动，市体育馆面向市民全面开放，实行收费优惠，具体收费标准如下：
①锻炼时间不超过1小时，免费；
②锻炼时间为1小时以上且不超过2小时，收费2元；
③锻炼时间为2小时以上且不超过3小时，收费3元；
④锻炼时间超过3小时的时段，按每小时3元收费（不足1小时的部分按1小时计算）已知甲、乙两人独立到体育馆锻炼一次，两人锻炼时间都不会超过3小时，设甲、乙锻炼时间不超过1小时的概率分别是0.4和0.5，锻炼时间为1小时以上且不超过2小时的概率分别是0.5和0.3．
（Ⅰ）求甲、乙两人所付费用相同的概率；
（Ⅱ）设甲、乙两人所付费用之和为随机变量ξ，求ξ的分布列和数学期望Eξ．
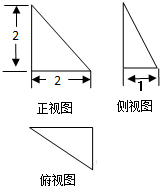已知某几何体的三视图如图所示，三个视图都为直角三角形，其中主视图是以2为直角边的等腰直角三角形，则该几何体的外接球的表面积为（　　）
A、16πB、9πC、8πD、4π
某校卫生所成立了调查小组，调查“按时刷牙与患龋齿的关系”，对该校某年级700名学生进行检查，按患龋齿和不患龋齿分类，得汇总数据：按时刷牙且不患龋齿的学生有60名，不按时刷牙但不患龋齿的学生有100名，按时刷牙但患龋齿的学生有140名．
（1）能否在犯错概率不超过0.01的前提下，认为该年级学生的按时刷牙与患龋齿有关系？
（2）4名校卫生所工作人员甲、乙、丙、丁被随机分成两组，每组2人，一组负责数据收集，
另一组负责数据处理，求工作人员甲分到“负责收集数据组”并且工作人员乙分到“负责数据处理组”的概率．
附：k2=
n(ad-bc)2
(a+b)(c+d)(a+c)(b+d)
P（K2≥k0）0.0100.0050.001
K06.635
 		7.879
 		10.828
 
?
已知函数f（x）=
(3-a)x-3(x≤7)
ax-6(x＞7)
若数列{an}满足an=f（n）（n∈N+），且{an}是递增数列，则实数a的取值范围是（　　）
A、[
9
4
，3）
B、（
9
4
，3）
C、（2，3）
D、（1，3）
设f（x）=
-x2+2x+1(x≥0)
e-x(x＜0)
关于x的方程f（x）=m（m∈R）恰有三个互不相等的实数根x1，x2，x3，则x1x2x3的取值范围是
 
．
为了对某课题进行研究，用分层取样方法从三所中学A，B，C的相关人员中，抽取若干人组成研究小组，有关数据见下表（单位：人）（1）求x，y（2）若从中学A，B抽取的人中选2人外出考察，求这二人都来自这些A的概率．
中学相关人员抽取人数
A30x
B20y
C101
已知函数F（x）=
f(x)
x
在定义域（0，+∞）内为单调增函数
（1）若f（x）=lnx+ax2，求a的取值范围
（2）设x0是f（x）的零点，m，n∈（0，x0），求证，
f(m+n)
f(m)+f(n)
＜1．
为了了解中学生的身体发育情况，对某中学17岁的60名女生的身高进行了测量，结果如下：154 159 166 169 159 156 166 162 158 167 156 166 160 164 160 157 151 157 161 162 158 153 158 164 158 163 158 153 157 163 162 159 154 165 166 157 151 146 157 158 160 165 158 163 163 162 161 154 165 159 162 159 157 159 149 164 168 159 153 160，根据数据列出样本的频率分布表，绘出频率直方图．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网