题目内容
8.已知函数f(x)=2sin(2x+$\frac{π}{6}$)+a+1,且当x$∈[0,\frac{π}{2}]$时,f(x)的最小值为2.(1)求a的值,并求(x)的单调递增区间;
(2)先将函数y=f(x)的图象上的点纵坐标不变,横坐标缩小到原来的$\frac{1}{2}$,再将所得的图象向右平移$\frac{π}{12}$个单位,得到函数y=g(x)的图象,求方程g(x)=4在区间[0,$\frac{π}{2}$]上所有根之和.
分析 (1)由条件利用正弦函数的定义域和值域,求得a的值.
(2)由题意利用正弦函数的图象可得sin(x+$\frac{π}{12}$)=$\frac{1}{2}$,由此求得它在区间[0,$\frac{π}{2}$]上所有根,从而得出结论
解答 解:(1)当x$∈[0,\frac{π}{2}]$时,2x+$\frac{π}{6}$∈[$\frac{π}{6}$,$\frac{7π}{6}$],故当2x+$\frac{π}{6}$=$\frac{7π}{6}$时,
函数f(x)=2sin(2x+$\frac{π}{6}$)+a+1的最小值为-1+a+1=2,∴a=2.
(2)先将函数y=f(x)的图象上的点纵坐标不变,横坐标缩小到原来的$\frac{1}{2}$,
可得y=2sin(x+$\frac{π}{6}$)+3的图象;
再将所得的图象向右平移$\frac{π}{12}$个单位,得到函数y=g(x)=2sin(x-$\frac{π}{12}$+$\frac{π}{6}$)+3=2sin(x+$\frac{π}{12}$)+3的图象,
方程g(x)=4在区间[0,$\frac{π}{2}$]上所有根之和,
即方程 sin(x+$\frac{π}{12}$)=$\frac{1}{2}$在区间[0,$\frac{π}{2}$]上所有根之和.
而方程 sin(x+$\frac{π}{12}$)=$\frac{1}{2}$在区间[0,$\frac{π}{2}$]上所有根满足x+$\frac{π}{12}$=$\frac{π}{6}$,即x=$\frac{π}{12}$,
故方程 sin(x+$\frac{π}{12}$)=$\frac{1}{2}$在区间[0,$\frac{π}{2}$]上所有根之和为$\frac{π}{6}$.
点评 本题主要考查正弦函数的定义域和值域,正弦函数的图象,属于基础题.

| A. | [-$\frac{π}{4}$,$\frac{π}{4}$] | B. | [0,$\frac{π}{4}$]∪($\frac{π}{2}$,$\frac{3π}{4}$] | C. | [0,$\frac{π}{4}$]∪[$\frac{3π}{4}$,π] | D. | [$\frac{π}{4}$,$\frac{3π}{4}$] |
| A. | -$\frac{1}{5}$i | B. | $\frac{1}{5}$i | C. | -i | D. | i |
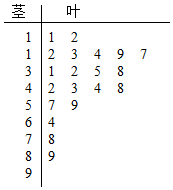 近期雾霾天气多发,对城市环境造成很大影响,某城市环保部门加强了对空气质量的检测,按国家环保部门发布的《环境空气质量标准》的规定:居民区的PM2.5(大气中直径小于或等于2.5微米的颗粒物)年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.抽取某居民区监控点记录的20天PM2.5的24小时平均浓度的监测数据,数集记录为如图茎叶图:
近期雾霾天气多发,对城市环境造成很大影响,某城市环保部门加强了对空气质量的检测,按国家环保部门发布的《环境空气质量标准》的规定:居民区的PM2.5(大气中直径小于或等于2.5微米的颗粒物)年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.抽取某居民区监控点记录的20天PM2.5的24小时平均浓度的监测数据,数集记录为如图茎叶图:(1)完成如下的频率分布表,并在所给的坐标系中画出(0,100)的频率分布直方图;
| 组别 | PM2.5浓度(微克/立方米) | 频数(天) | 频率 |
| 第一组 | (0,25] | ||
| 第二组 | (25,50] | ||
| 第三组 | (50,75] | ||
| 第四组 | (75,100] |
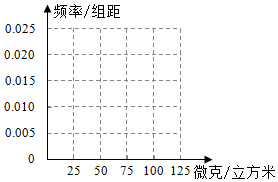 (2)从样本中PM2.5的24小时平均浓度超过50微克/立方米的5天中,求恰好有一天PM2.5的24小时平均浓度超过75微克/立方米的概率.
(2)从样本中PM2.5的24小时平均浓度超过50微克/立方米的5天中,求恰好有一天PM2.5的24小时平均浓度超过75微克/立方米的概率.