题目内容
若关于x的不等式ax2+bx+c<0的解集是{x|x<-2或x>-1},则关于x的不等式cx2+bx+a>0的解集是 .
考点:一元二次不等式的解法
专题:不等式的解法及应用
分析:由不等式ax2+bx+c<0的解集求出a、b、c的关系,再把不等式cx2+bx+a>0化为可以解答的一元二次不等式,求出解集即可.
解答:
解:∵关于x的不等式ax2+bx+c<0的解集是{x|x<-2或x>-1},
∴关于x的方程ax2+bx+c=0有两个实数根是x=-2或x=-1;
∴a<0且
,
∴c<0,且
;
∴关于x的不等式cx2+bx+a>0可化为
x2+
x+
<0,
即x2+
x+
<0;
解得-1<x<-
,
∴该不等式的解集是{x|-1<x<-
}.
故答案为:{x|-1<x<-
}.
∴关于x的方程ax2+bx+c=0有两个实数根是x=-2或x=-1;
∴a<0且
|
∴c<0,且
|
∴关于x的不等式cx2+bx+a>0可化为
x2+
| b |
| c |
| a |
| c |
即x2+
| 3 |
| 2 |
| 1 |
| 2 |
解得-1<x<-
| 1 |
| 2 |
∴该不等式的解集是{x|-1<x<-
| 1 |
| 2 |
故答案为:{x|-1<x<-
| 1 |
| 2 |
点评:本题考查了一元二次不等式的解法与应用问题,也考查了根与系数的关系问题,是综合题.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
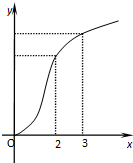 已知函数f(x)的图象如图所示,f′(x)是f(x)的导函数,则下列数值排序正确的是( )
已知函数f(x)的图象如图所示,f′(x)是f(x)的导函数,则下列数值排序正确的是( )A、0<f′(2)<f′(3)<
| ||
B、0<f′(3)<
| ||
C、0<f′(3)<f′(2)<
| ||
D、0<
|
(文科)已知-3<a<-2,3<b<4,则
的取值范围为( )
| a2 |
| b |
| A、(1,3) | ||||
B、(
| ||||
C、(
| ||||
D、(
|
设全集U={1,2,3,4,5,6,7},集合A={1,3,5},集合B={2,4,5},则(∁UA)∩B=( )
| A、{1,3,5} |
| B、{1,5} |
| C、{2,4} |
| D、{2,4,6} |
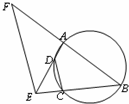 如图,A、B,C,D四点在同一圆上,BC与AD的延长线交于点E,点F在BA的延长线上.
如图,A、B,C,D四点在同一圆上,BC与AD的延长线交于点E,点F在BA的延长线上.