题目内容
如图所示,在△DEM中,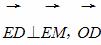 =(0,-8),N在y轴上,且
=(0,-8),N在y轴上,且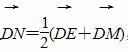 点E在x轴上移动.
点E在x轴上移动.
(1)求点M的轨迹方程;
(2)过点F(0,1)作互相垂直的两条直线l1、l2,l1与点M的轨迹交于点A、B,l2与点M的轨迹交于点C、Q,求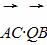 的最小值.
的最小值.
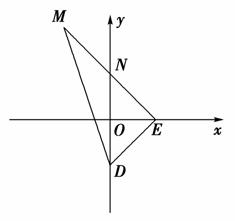
(1)设M(x,y),E(a,0),由条件知D(0,-8),
∵N在y轴上且N为EM的中点,∴x=-a,
∵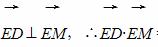 =(-a,-8)·(x-a,y)=-a(x-a)-8y=2x2-8y=0,∴x2=4y(x≠0),
=(-a,-8)·(x-a,y)=-a(x-a)-8y=2x2-8y=0,∴x2=4y(x≠0),
∴点M的轨迹方程为x2=4y(x≠0).
(2)设A(x1,y1),B(x2,y2),C(x3,y3),Q(x4,y4),直线l1:y=kx+1(k≠0),则直线l2:y=-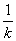 x+1,
x+1,
由 消去y得,x2-4kx-4=0,
消去y得,x2-4kx-4=0,
∴x1+x2=4k,x1x2=-4,
由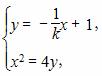 消去y得,x2+
消去y得,x2+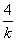 x-4=0,
x-4=0,
∴x3+x4=-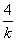 ,x3x4=-4.
,x3x4=-4.
∵A、B在直线l1上,∴y1=kx1+1,y2=kx2+1,
∵C、Q在直线l2上,∴y3=-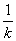 x3+1,y4=-
x3+1,y4=-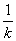 x4+1.
x4+1.
∴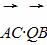 =(x3-x1,y3-y1)·(x2-x4,y2-y4)
=(x3-x1,y3-y1)·(x2-x4,y2-y4)
=(x3-x1)(x2-x4)+(y3-y1)·(y2-y4)
=(x3-x1)(x2-x4)+(-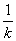 x3-kx1)(kx2+
x3-kx1)(kx2+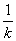 x4)
x4)
=x3x2-x1x2-x3x4+x1x4-x2x3-k2x1x2-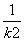 x3x4-x1x4
x3x4-x1x4
=(-1-k2)x1x2+(-1-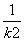 )x3x4=4(1+k2)+4(1+
)x3x4=4(1+k2)+4(1+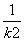 )=8+4(k2+
)=8+4(k2+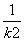 )≥16等号在k2=
)≥16等号在k2=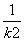 时取得,
时取得,
即k=±1时成立.∴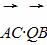 的最小值为16.
的最小值为16.

练习册系列答案
相关题目
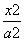 +
+ =1(a>b>0)的两焦点,P是椭圆上任一点,过一焦点引∠F1PF2的外角平分线的垂线,则垂足Q的轨迹为( )
=1(a>b>0)的两焦点,P是椭圆上任一点,过一焦点引∠F1PF2的外角平分线的垂线,则垂足Q的轨迹为( )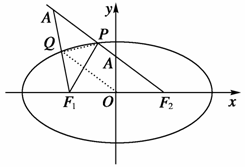
 为奇函数,则常数
为奇函数,则常数 = ;
= ;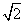 x的焦点,P为C上一点,若|PF|=4
x的焦点,P为C上一点,若|PF|=4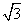 D.4
D.4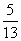 ,焦点在x轴上且长轴长为26.若曲线C2上的点到椭圆C1的两个焦点的距离的差的绝对值等于8,则曲线C2的标准方程为( )
,焦点在x轴上且长轴长为26.若曲线C2上的点到椭圆C1的两个焦点的距离的差的绝对值等于8,则曲线C2的标准方程为( )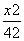 -
-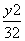 =1 B.
=1 B.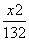 -
-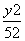 =1
=1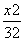 -
-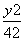 =1 D.
=1 D.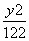 =1
=1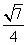 的直线l,交双曲线左支于A、B两点,交y轴于点C,且满足|PA|·|PB|=|PC|2.
的直线l,交双曲线左支于A、B两点,交y轴于点C,且满足|PA|·|PB|=|PC|2.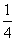 上一动点,求|MN|的取值范围.
上一动点,求|MN|的取值范围.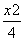 -y2=1上一动点,O为坐标原点,M为线段OP的中点,则点M的轨迹方程是________.
-y2=1上一动点,O为坐标原点,M为线段OP的中点,则点M的轨迹方程是________.