题目内容
已知动圆过定点A(4,0),且在y轴上截得弦长MN的长为8.
(1)求动圆圆心的轨迹C的方程;
(2)已知点B(-1,0),设不垂直于x轴的直线l与轨迹C交于不同的两点P,Q,若x轴是∠PBQ的角平分线,证明直线l过定点.
(1)
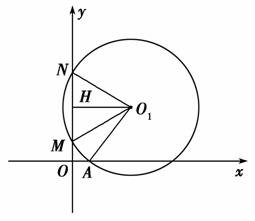
如图,设动圆的圆心O1(x,y),由题意知|O1A|=|O1M|,当O1不在y轴上时,过O1作O1H⊥MN交MN于H,则H为MN的中点,
∴|O1M|2=|O1H|2+|MH|2=x2+16,
又|O1A|2=(x-4)2+y2,
∴(x-4)2+y2=x2+16,整理得y2=8x(x≠0),
当O1在y轴上时,∵|OA|=4=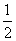 |MM|,
|MM|,
∴O1与O重合,此时点O1(0,0)也满足y2=8x,
∴动圆圆心O1的轨迹C方程为y2=8x.
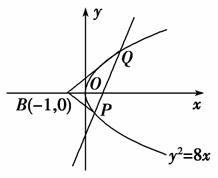
(2)证明:由题意,设直线l的方程为y=kx+b(k≠0),
P(x1,y1),Q(x2,y2),
将y=kx+b代入y2=8x中,
得k2x2+(2bk-8)x+b2=0,
其中Δ=-32kb+64>0.
由根与系数的关系得,x1+x2=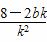 ,①
,①
x1x2=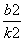 ,②
,②
因为x轴是∠PBQ的角平分线,
所以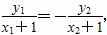 ,
,
即y1(x2+1)+y2(x1+1)=0,
(kx1+b)(x2+1)+(kx2+b)(x1+1)=0,
2kx1x2+(b+k)(x1+x2)+2b=0,③
将①,②代入③得2kb2+(k+b)(8-2bk)+2k2b=0,
∴k=-b,此时Δ>0,∴直线l的方程为y=k(x-1),
即直线l过定点(1,0).

练习册系列答案
相关题目
 B.
B.

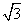 x-4的距离的最小值是________.
x-4的距离的最小值是________.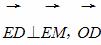 =(0,-8),N在y轴上,且
=(0,-8),N在y轴上,且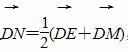 点E在x轴上移动.
点E在x轴上移动.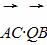 的最小值.
的最小值.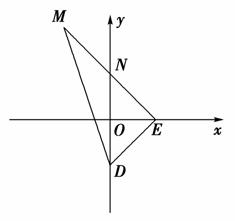
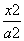 -
-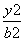 =1(a>0,b>0)的一条渐近线方程是y=
=1(a>0,b>0)的一条渐近线方程是y=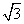 x,它的一个焦点在抛物线y2=48x的准线上.则双曲线的方程为( )
x,它的一个焦点在抛物线y2=48x的准线上.则双曲线的方程为( )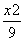 -
-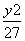 =1 B.
=1 B.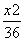 -
-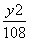 =1
=1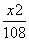 -
-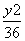 =1 D.
=1 D.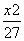 -
-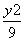 =1
=1 =1的右顶点为A,右焦点为F.过点F平行于双曲线的一条渐近线的直线与双曲线交于点B,则△AFB的面积为________.
=1的右顶点为A,右焦点为F.过点F平行于双曲线的一条渐近线的直线与双曲线交于点B,则△AFB的面积为________.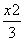 -
-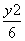 =1 B.
=1 B.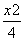 -
-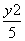 =1
=1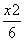 -
-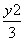 =1 D.
=1 D. -
- =1
=1