题目内容
17.已知等差数列{an}中,a5=9,a7=13,等比数列{bn}的通项公式bn=2n-1,n∈N*.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{an+bn}的前n项和Sn.
分析 (Ⅰ)设等差数列{an}的公差为d,运用等差数列的通项公式列方程组,解方程组可得首项和公差,进而得到所求通项公式;
(Ⅱ)分组求和,结合等差数列和等比数列的求和公式即可得到所求和.
解答 解(I)由题知$\left\{\begin{array}{l}{{a}_{5}={a}_{1}+4d=9}\\{{a}_{7}={a}_{1}+6d=13}\end{array}\right.$,
解得a1=1,d=2,
∴an=2n-1,n∈N*,.
(II)由(I)知,an+bn=(2n-1)+2n-1,
由于{an}的前n项和为$\frac{n(1+2n-1)}{2}$=n2,
∵${b_n}={2^{n-1}},n∈{N^*}$.
∴{bn}是以1为首项,以2为公比的等比数列,
∴数列{bn}的前n项和为$\frac{1×(1-{2}^{n})}{1-2}$=2n-1,
∴{an+bn}的前n项和Sn=n2+2n-1
点评 本题考查等差数列的通项公式和求和公式的运用,考查数列的求和方法:分组求和,考查运算能力,属于中档题.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
7.已知a≥2,f(x)=x3+3|x-a|,若函数f(x)在[-1,1]上的最大值和最小值分别记为M,m,则M-m的值为( )
| A. | 8 | B. | -a3-3a+4 | C. | 4 | D. | -a3+3a+2 |
8.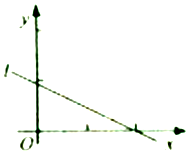 设(x1,y1),(x2,y2),…,(xn,yn)是变量x和y的n个样本点,直线l是由这些样本点通过最小二乘法得到的线性回归直线(如图),以下结论中正确的是( )
设(x1,y1),(x2,y2),…,(xn,yn)是变量x和y的n个样本点,直线l是由这些样本点通过最小二乘法得到的线性回归直线(如图),以下结论中正确的是( )
 设(x1,y1),(x2,y2),…,(xn,yn)是变量x和y的n个样本点,直线l是由这些样本点通过最小二乘法得到的线性回归直线(如图),以下结论中正确的是( )
设(x1,y1),(x2,y2),…,(xn,yn)是变量x和y的n个样本点,直线l是由这些样本点通过最小二乘法得到的线性回归直线(如图),以下结论中正确的是( )| A. | x和y的相关系数在-1和0之间 | |
| B. | x和y的相关系数为直线l的斜率 | |
| C. | 当n为偶数时,分布在l两侧的样本点的个数一定相同 | |
| D. | 所有样本点(xi,yi)(i=1,2,…,n)都在直线l上 |
12.下列命题正确的是( )
| A. | 若ac>bc,则a>b | B. | 若a>b,c>d,则ac>bd | ||
| C. | 若a>b,则$\frac{1}{a}<\frac{1}{b}$ | D. | 若ac2>bc2,则a>b |
6.若△ABC的内角A,B,C满足$\frac{sinA}{2}$=$\frac{sinB}{4}$=$\frac{sinC}{3}$,则cosB=( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{1}{4}$ |
7.已知某空间几何体的三视图如图所示,则该几何体的体积为( )
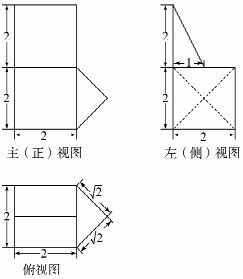

| A. | $\frac{40}{3}$ | B. | $\frac{34}{3}$ | C. | $10+\frac{{4\sqrt{2}}}{3}$ | D. | $6+\frac{{4\sqrt{3}}}{3}$ |