Question

【题目】如图，扇形OAB的半径为1，圆心角为120°，四边形PQRS是扇形的内接矩形，当其面积最大时，求点P的位置，并求此最大面积．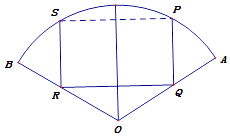

Answer 1

【答案】解：设SP中点为C，PQ中点为D，如图所示；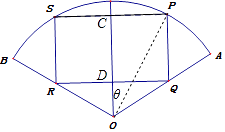

设∠COP=θ，则CP=1×sinθ=sinθ，
CO=cosθ，
DQ=CP=sinθ，
又∠DOQ= ，
∴OD= ，
∴CD=OC﹣OD=cosθ﹣ ，
∴S四边形PQRS=CD×SP
=（cosθ﹣ ）2sinθ
=sin2θ﹣
=sinθ﹣
=sin2θ+ cos2θ﹣
= sin（2θ+ ）﹣ ，
当θ= 时，四边形SPQR取得最大值为
Smax= ，
此时点P在弧AB的四等分点处
【解析】根据题意，设SP中点为C，PQ中点为D，∠COP=θ，表示出四边形SPRS的面积，再利用三角恒等变换求出它的最大值即可．
【考点精析】根据题目的已知条件，利用扇形面积公式的相关知识可以得到问题的答案，需要掌握若扇形的圆心角为，半径为，弧长为，周长为，面积为，则，，．