题目内容
已知O为坐标原点,向量
=(1,0),
=(-1,2).若平面区域D由所有满足
=λ
+μ
(-2≤λ≤2,-1≤μ≤1)的点C组成,则能够把区域D的周长和面积同时分为相等的两部分的曲线是( )
| OA |
| OB |
| OC |
| OA |
| OB |
A、y=
| ||
| B、y=x+cosx | ||
C、y=ln
| ||
| D、y=ex+e-x-1 |
考点:平面向量的基本定理及其意义,函数的图象
专题:平面向量及应用
分析:设C(x,y),由
=λ
+μ
(-2≤λ≤2,-1≤μ≤1),可得
.由-2≤λ≤2,-1≤μ≤1,可得-2≤y≤2,x+
=λ∈[-2,2].可得如图所示的平面区域D关于原点对称.所给的函数中:满足能够把区域D的周长和面积同时分为相等的两部分,则函数必须是奇函数且经过原点.
| OC |
| OA |
| OB |
|
| y |
| 2 |
解答:
解:设C(x,y),∵
=λ
+μ
(-2≤λ≤2,-1≤μ≤1),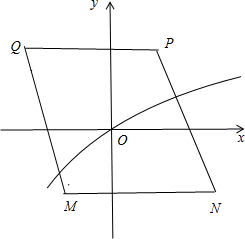
∴(x,y)=λ(1,0)+μ(-1,2),
∴
.
∵-2≤λ≤2,-1≤μ≤1,
∴-2≤y≤2,x+
=λ∈[-2,2].
可得如图所示的平面区域D关于原点对称.
所给的函数中:只有C中的函数y=ln
是奇函数且经过原点,
满足能够把区域D的周长和面积同时分为相等的两部分.
故选:C.
| OC |
| OA |
| OB |

∴(x,y)=λ(1,0)+μ(-1,2),
∴
|
∵-2≤λ≤2,-1≤μ≤1,
∴-2≤y≤2,x+
| y |
| 2 |
可得如图所示的平面区域D关于原点对称.
所给的函数中:只有C中的函数y=ln
| 5-x |
| 5+x |
满足能够把区域D的周长和面积同时分为相等的两部分.
故选:C.
点评:本题考查了向量的线性运算、线性规划有关知识、奇函数的性质,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
已知F1、F2分别是双曲线C1:
-
=1(a>0,b>0)的左右焦点,且F2是抛物线C2:y2=2px(p>0)的焦点,双曲线C1与抛物线C2的一个公共点是P,若线段PF2的中垂线恰好经过焦点F1,则双曲线C1的离心率是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、2+
| ||
B、1+
| ||
C、2+
| ||
D、1+
|
直线m⊥平面α,垂足是O,正四面体ABCD的棱长为4,点C在平面α上运动,点B在直线m上运动,则点O到直线AD的距离的取值范围是( )
A、[
| ||||||||
B、[2
| ||||||||
C、[
| ||||||||
D、[3
|
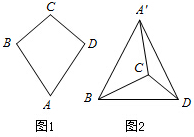 如图1,已知四边形ABCD的对角线AC与BD互相垂直,∠A=60°,∠C=90°,CD=CB=2,将△ABD沿BD折起,得到三棱锥A′-BCD,如图2.
如图1,已知四边形ABCD的对角线AC与BD互相垂直,∠A=60°,∠C=90°,CD=CB=2,将△ABD沿BD折起,得到三棱锥A′-BCD,如图2.