题目内容
函数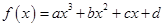 的图象(如图),则函数
的图象(如图),则函数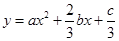 的单调递增区间是( )
的单调递增区间是( )

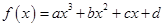 的图象(如图),则函数
的图象(如图),则函数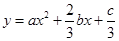 的单调递增区间是( )
的单调递增区间是( )
A.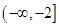 | B.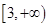 |
C.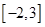 | D.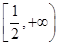 |
D
试题分析:因为函数
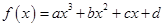 ,则f'(x)=3ax2+2bx+c,由图可知f'(-2)=0,f'(3)=0,∴12a-4b+c=0,27a+6b+c=0,∴b=-
,则f'(x)=3ax2+2bx+c,由图可知f'(-2)=0,f'(3)=0,∴12a-4b+c=0,27a+6b+c=0,∴b=- ,c=-18a,所以
,c=-18a,所以  ,则y’=a(2x-1)
,则y’=a(2x-1)∴y=3ax2-3ax-18a,结合图像可知a>0,那么y'=a(2x-1),当x>
 时,y'>0,∴y=x2-x-6的单调递增区间为:[
时,y'>0,∴y=x2-x-6的单调递增区间为:[ ,+∞),故选D.
,+∞),故选D.点评:解决该试题的关键是通过图像确定出-2和3为函数的极值点,那么导数值为零,从而得到a,b,c,的关系式进而化简函数,求解导数得到单调区间。

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
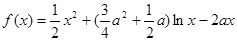 ,
, .
.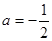 时,求函数
时,求函数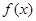 的极值点;
的极值点;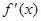 的单调区间上也是单调的,求
的单调区间上也是单调的,求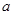 的取值范围;
的取值范围;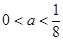 时,设
时,设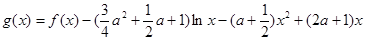 ,且
,且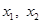 是函数
是函数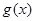 的极值点,证明:
的极值点,证明: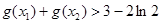 .
.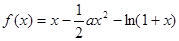 ,其中
,其中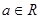 .
.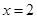 是
是 的极值点,求
的极值点,求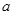 的值;
的值;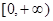 上的最大值是
上的最大值是 ,求
,求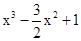 (2)
(2)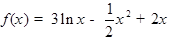
 (
( ),当
),当 时函数
时函数 的极值为
的极值为 ,则
,则 .
.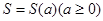 是图1中阴影部分介于平等线
是图1中阴影部分介于平等线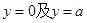 之间的那一部分的面积,则函数
之间的那一部分的面积,则函数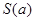 的图象大致为( )
的图象大致为( )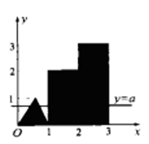
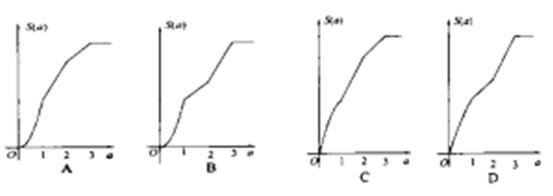
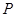 在曲线
在曲线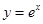 上,点
上,点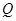 在曲线
在曲线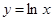 上,则
上,则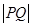 的最小值是
的最小值是  与时间t(
与时间t( )的关系近似表示为
)的关系近似表示为 ,则汽车在时刻
,则汽车在时刻 秒时的加速度为 ( )
秒时的加速度为 ( )

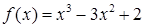 在区间
在区间 上的最大值是_________.
上的最大值是_________.