题目内容
本题满分15分)已知函数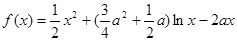 ,
, .
.
(Ⅰ)当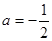 时,求函数
时,求函数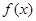 的极值点;
的极值点;
(Ⅱ)若函数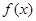 在导函数
在导函数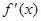 的单调区间上也是单调的,求
的单调区间上也是单调的,求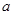 的取值范围;
的取值范围;
(Ⅲ) 当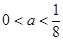 时,设
时,设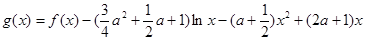 ,且
,且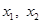 是函数
是函数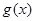 的极值点,证明:
的极值点,证明: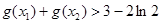 .
.
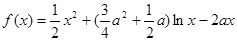 ,
, .
.(Ⅰ)当
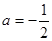 时,求函数
时,求函数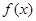 的极值点;
的极值点;(Ⅱ)若函数
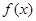 在导函数
在导函数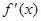 的单调区间上也是单调的,求
的单调区间上也是单调的,求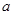 的取值范围;
的取值范围;(Ⅲ) 当
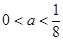 时,设
时,设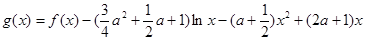 ,且
,且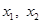 是函数
是函数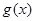 的极值点,证明:
的极值点,证明: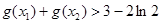 .
.(Ⅰ) 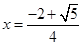 (Ⅱ)
(Ⅱ) 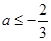 或
或 (Ⅲ)见解析
(Ⅲ)见解析
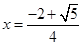 (Ⅱ)
(Ⅱ) 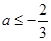 或
或 (Ⅲ)见解析
(Ⅲ)见解析试题分析:(Ⅰ)当
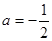 时,
时,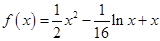 (
(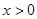 ),
),令
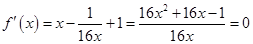 ,
,解得
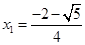 (舍),
(舍),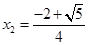 , ……1分
, ……1分容易判断出函数在区间
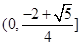 单调递减,在区间
单调递减,在区间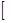
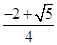 ,+∞)上单调递增
,+∞)上单调递增……2分
∴
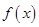 在
在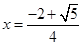 时取极小值. ……4分
时取极小值. ……4分(Ⅱ)解法一:
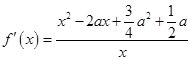
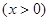 ……5分
……5分令
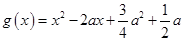 ,
,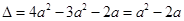 ,设
,设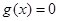 的两根为
的两根为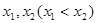 ,
,10当
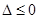 即
即 ,
,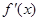 ≥0,∴
≥0,∴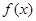 单调递增,满足题意. ……6分
单调递增,满足题意. ……6分20当
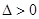 即
即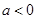 或
或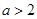 时,
时,(1)若
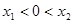 ,则
,则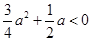 ,即
,即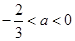 时,
时,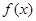 在
在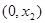 上递减,
上递减,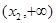 上递增,
上递增,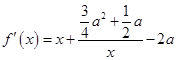 ,
,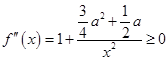 ∴
∴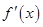 在(0,+∞)单调增,不合题意. ……7分
在(0,+∞)单调增,不合题意. ……7分(2)若
 则
则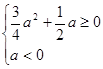 ,即
,即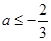 时
时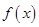 在(0,+∞)上单调增,满足题意.
在(0,+∞)上单调增,满足题意.……8分
(3) 若
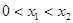 则
则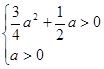 即a>2时
即a>2时∴
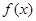 在(0,
在(0,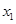 )上单调递增,在(
)上单调递增,在(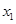 ,
, )上单调递减,在(
)上单调递减,在( ,+∞)上单调递增,
,+∞)上单调递增,不合题意. ……9分
综上得
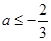 或
或 . ……10分
. ……10分解法二:
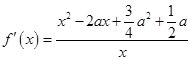 , ……5分
, ……5分令
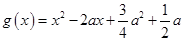 ,
,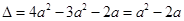 ,
,设
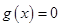 的两根
的两根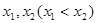
10当
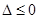 即
即 ,
,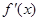 ≥0,∴
≥0,∴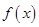 单调递增,满足题意. ……6分
单调递增,满足题意. ……6分20当
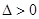 即
即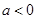 或
或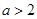 时,
时, (1)当
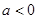 若
若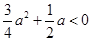 ,即
,即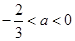 时,
时,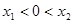 ,
,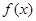 在
在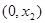 上单调递减,在
上单调递减,在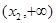 上单调递增,
上单调递增, 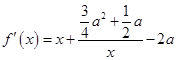 ,
,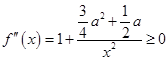 ∴
∴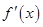 在(0,+∞)单调增不合题意. ……7分
在(0,+∞)单调增不合题意. ……7分若
 ,即
,即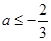 时,
时, f(x)在(0,+∞)上单调增,满足题意.
f(x)在(0,+∞)上单调增,满足题意.……8分
(2)当
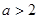 时,
时, ,
,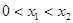
∴f(x)在(0,x1)单调增,(x1,x2)单调减,(x2,+∞)单调增,不合题意 ……9分
综上得
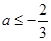 或
或 . ……10分
. ……10分(Ⅲ)
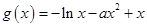 ,
,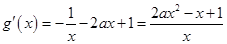
令
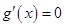 ,即
,即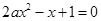 ,当
,当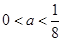 时,
时,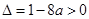 ,
,所以,方程
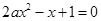 有两个不相等的正根
有两个不相等的正根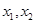 ,
,不妨设
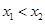 ,则当
,则当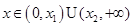 ,
,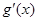 <0,
<0,当
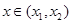 时,
时,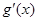 >0, ……11分 所以,
>0, ……11分 所以,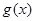 有极小值点
有极小值点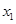 和极大值点
和极大值点 ,且
,且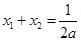 ,
,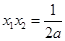 .
.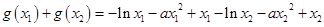
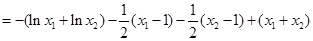
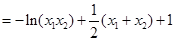
 . ……13分
. ……13分令
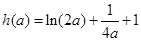 ,
,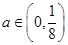 ,
,则当
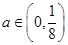 时,
时,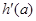 =
=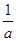 -
-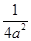 =
=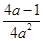 <0,
<0,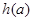 在
在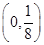 )单调递减,……14分所以
)单调递减,……14分所以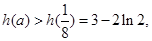 即
即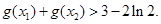 ……15分
……15分点评:新课标对有关函数的综合题的考查,重在对函数与导数知识理解的准确性、深刻性,重在与方程、不等式等相关知识的相互联系,要求学生具备较高的数学思维能力以及较强的运算能力,体现了以函数为载体,多种能力同时考查的命题思想.

练习册系列答案
相关题目
 记
记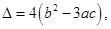 则当
则当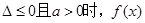 的大致图像为( )
的大致图像为( )
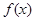 的图象如图所示,则不等式
的图象如图所示,则不等式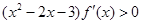 的解集为( )
的解集为( )
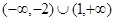
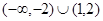
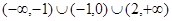
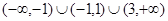
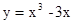 ,则它的单调减区间是
,则它的单调减区间是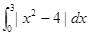 = ( )
= ( )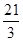

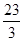
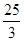
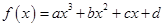 的图象(如图),则函数
的图象(如图),则函数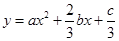 的单调递增区间是( )
的单调递增区间是( )
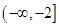
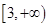
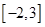
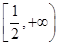
 在
在 处有极值,则函数
处有极值,则函数 的图象在
的图象在 处的切线的斜率为( )
处的切线的斜率为( )



 经过点
经过点 、
、 与
与 ,
, ,
, ,设函数
,设函数 在
在 和
和 处取到极值.
处取到极值. 表示
表示 的大小(要求按从小到大排列);
的大小(要求按从小到大排列); ,且过原点存在两条互相垂直的直线与曲线
,且过原点存在两条互相垂直的直线与曲线 均相切,求
均相切,求