题目内容
设m,n∈R,若直线(m+1)x+(n+1)y-2=0与圆(x-1)2+(y-1)2=1相切,则m+n的取值范围是( )
A.[1- ,1+ ,1+ ] ] |
B.(-∞,1- ]∪[1+ ]∪[1+ ,+∞) ,+∞) |
C.[2-2 ,2+2 ,2+2 ] ] |
D.(-∞,2-2 ]∪[2+2 ]∪[2+2 ,+∞) ,+∞) |
D
圆心(1,1)到直线(m+1)x+(n+1)y-2=0的距离为 =1,
=1,
所以m+n+1=mn≤ (m+n)2,
(m+n)2,
所以m+n≥2+2 或m+n≤2-2
或m+n≤2-2 .
.
 =1,
=1,所以m+n+1=mn≤
 (m+n)2,
(m+n)2,所以m+n≥2+2
 或m+n≤2-2
或m+n≤2-2 .
.
练习册系列答案
 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目

 B.2 C.3 D.2
B.2 C.3 D.2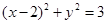 的圆心,圆上有一点
的圆心,圆上有一点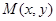 满足
满足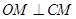 ,则
,则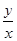 = ( )
= ( )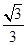
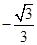
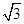
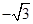
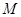 :
: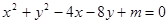 与
与 轴相切,点
轴相切,点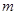 的值;
的值;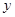 轴上截得的弦长;
轴上截得的弦长; 是直线
是直线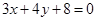 上的动点,过点
上的动点,过点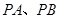 与圆
与圆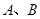 为切点.求四边形
为切点.求四边形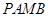 面积的最小值。
面积的最小值。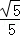
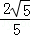
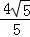
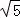
 的一条切线与
的一条切线与 轴、
轴、 轴分别交于点
轴分别交于点 , 则
, 则 的最小值为( )
的最小值为( )
 交圆于F,若CB=2,CE=4,则AD的长为 .
交圆于F,若CB=2,CE=4,则AD的长为 .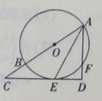
 出发经
出发经 轴反射到圆C:
轴反射到圆C: 上的最短路程是 .
上的最短路程是 .