题目内容
11.如图所示,已知OA⊥?ABCD所在的平面,P、Q分别是AB,OC的中点,求证:PQ∥平面OAD.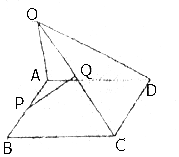
分析 取OD中点G,连接AG、QG,利用三角形中位线定理,我们易判断四边形APQG是平行四边形,AG∥PQ,进而结合线面平行的判定定理,我们易得到PQ∥平面OAD.
解答 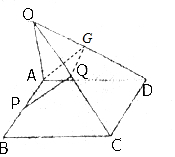 证明:取OD中点G,连接AG、QG,
证明:取OD中点G,连接AG、QG,
因为EF分别为AB、PC的中点,
所以AP=$\frac{1}{2}$AB,GQ∥DC且GQ=$\frac{1}{2}$DC,
又在平行四边形ABCD中AB∥CD且AB=CD,
所以AP∥GQ且AP=GQ,
所以四边形APQG是平行四边形,
所以AG∥PQ且AG=PQ
又,AG?平面OAD,PQ?平面OAD.
所以PQ∥平面OAD.
点评 本题考查的知识点是直线与平面平行的判定,熟练掌握判定定理内容及解题步骤是解答此类问题的关键.

练习册系列答案
相关题目
16.已知直线y=kx+1与曲线y=x3+mx+n相切于点P(1,3),则n=( )
| A. | -1 | B. | 1 | C. | 3 | D. | 4 |
16.已知集合P={x∈N|1≤x<10},集合Q={x∈R|x2+x-6=0},则P∩Q=( )
| A. | {2} | B. | {3} | C. | {-2,3} | D. | .{-3,2} |