题目内容
15.如图,圆柱高为2,底面半径为1,则在圆柱侧面上从A出发经过母线BB1到达A1的最短距离为2$\sqrt{{π}^{2}+1}$.
分析 将圆柱侧面展开得到一个矩形,根据两点之间线段最短,求出对角线长即可.
解答 解:因为圆柱底面圆的周长为2π×1=2π,高为2,
所以将侧面展开为一长为2π,宽为2的矩形,
根据勾股定理,对角线长为$\sqrt{4{π}^{2}+4}$=2$\sqrt{{π}^{2}+1}$.
故在圆柱侧面上从A出发经过母线BB1到达A1的最短距离为2$\sqrt{{π}^{2}+1}$.
点评 此题考查了圆柱的侧面展开图和勾股定理,需要同学们有一定的空间思维能力.

练习册系列答案
相关题目
6.把45化为二进制数为( )
| A. | 1011112 | B. | 1011012 | C. | 1101012 | D. | 1111012 |
3.某几何体的三视图如图所示,则该几何体的表面积是( )
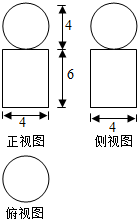

| A. | 44π | B. | 48π | C. | $\frac{116π}{3}$ | D. | $\frac{128π}{3}$ |
10.已知定义在R上的函数y=f(x)满足以下三个条件:
①对于任意的x∈R,都有f(x+4)=f(x);
②对于任意的x1,x2∈R,且0≤x1<x2≤2,都有f(x1)<f(x2);
③函数y=f(x+2)的图象关于y轴对称
则下列结论中正确的是( )
①对于任意的x∈R,都有f(x+4)=f(x);
②对于任意的x1,x2∈R,且0≤x1<x2≤2,都有f(x1)<f(x2);
③函数y=f(x+2)的图象关于y轴对称
则下列结论中正确的是( )
| A. | f (4.5)<f (7)<f (6.5) | B. | f (7)<f (4.5)<f (6.5) | C. | f (7)<f (6.5)<f (4.5) | D. | f (4.5)<f (6.5)<f (7) |
20.不等式|2x-1|≤7的解集是( )
| A. | {x|x≥-3} | B. | {x|x≤4} | C. | {x|-3≤x≤4} | D. | {x|x≤-3或x≥4} |