题目内容

求证：
tanα
tanβ
=
sin(α+β)+sin(α-β)
sin(α+β)-sin(α-β)
．
考点：两角和与差的正弦函数
专题：三角函数的求值
分析：由两角和与差的正弦函数展开右边，由正切公式可证．
解答： 证明：右边=
sinαcosβ+cosαsinβ+sinαcosβ-cosαsinβ
sinαcosβ+cosαsinβ-sinαcosβ+cosαsinβ

=
2sinαcosβ
2cosαsinβ
=
sinα
cosα
•
cosβ
sinβ
=
tanα
tanβ
=左边
命题得证
点评：本题考查两角和与差的正弦函数，涉及正切公式，属基础题．
练习册系列答案
相关题目
函数y=sin（2x+
π
6
）在x∈[-
π
6
，
π
3
]上的值域为
 
．
已知数列{an}满足a1=1，an=
2
S
2
n
2Sn-1
（n≥2）．
（1）求证：数列{
1
Sn
}为等差数列；
（2）求{an}的通项公式．
已知f（x）是定义在R上连续的偶函数，f（x）的图象向右平移一个单位长度又得到一个奇函数，且f（2）=-1，则f（8）+f（9）+f（10）+…+f（2012）+f（2013）+f（2014）=
 
．
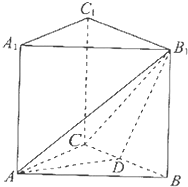如图，在棱长均相等的正三棱柱ABC-A1B1C1中，D为BC的中点．
（1）求证：A1B∥平面AC1D；
（2）求C1C与平面AC1D所成角的余弦值．
已知函数f（x）=2cos（
π
2
-
π
4
x-
π
4
）．
（1）求函数f（x）图象的对称轴；
（2）将函数f（x）的图象上所有的点向左平移1个单位长度，得到函数g（x）的图象，若函数y=g（x）+k在（-2，4）上有两个零点，求实数k的取值范围．
已知角θ的终边经过点P（-4cosα，3cosα），α∈{α|π＜α＜2π，α≠
3π
2
}，则sinθ+cosθ=
 
．
对于给定的函数f（x）=2x-2-x，有下列四个结论：
①f（x）的图象关于原点对称；
②f（x）在R上是增函数；
③f（x）的图象关于y轴对称；
④f（x）的最小值为0．
其中正确的个数有（　　）
A、4个B、3个C、2个D、1个
正四棱柱ABCD-A1B1C1D1中，底面ABCD是边长为4的正方形，A1C1与B1D1交于点N，BC1与B1C交于点M，且AM⊥BN，建立空间直角坐标系．
（1）求AA1的长；
（2）求＜
BN
，
AD1
＞；
（3）对于n个向量
a1
，
a2
，…，
an
，如果存在不全为零的n个实数λ1，λ2，…，λn，使得λ1
a1
+λ2
a2
+…+λn
an
=0成立，则这n个向量
a1
，
a2
，…，
an
叫做线性相关，不是线性相关的向量叫线性无关，判断
AM
，
BN
，
CD
是否线性相关，并说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网