题目内容
5.若曲线y=x2-x+2与直线y=x+m有两个交点,则实数m的取值范围是m>1.分析 曲线y=x2-x+2与直线y=x+m有两个交点,x2-2x+2-m=0有两个根,△>0,从而可求得m的取值范围.
解答 解:∵曲线y=x2-x+2与直线y=x+m有两个交点,
∴x2-2x+2-m=0有两个根
∴△>0,即(-2)2-4×(2-m)>0.
整理得:m-1>0.
解得:m>1.
故答案为:m>1.
点评 本题主要考查的是抛物线与直线的交点,明确当△>0,x2-2x+2-m=0有两个根是解题的关键.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
15.集合{y∈z|0<y≤4}的子集个数是( )
| A. | 64 | B. | 32 | C. | 16 | D. | 8 |
13.数列{an}的前n项和为Sn,若an=$\frac{1}{n(n+1)}$,则S19等于( )
| A. | $\frac{18}{19}$ | B. | $\frac{20}{19}$ | C. | $\frac{19}{20}$ | D. | $\frac{21}{20}$ |
5.某人有5把钥匙,其中2把能打开门.现随机取钥匙试着开门,不能开门就扔掉.则恰好在第3次才能开门的概率为( )
| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{3}{10}$ | D. | $\frac{2}{5}$ |
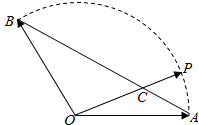 如图,已知不共线的两个单位向量$\overrightarrow{OA}$、$\overrightarrow{OB}$的夹角为120°,点C在线段AB上,设向量$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$(x,y∈R).
如图,已知不共线的两个单位向量$\overrightarrow{OA}$、$\overrightarrow{OB}$的夹角为120°,点C在线段AB上,设向量$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$(x,y∈R).