题目内容
已知圆 ,直线
,直线  ,
, 与圆
与圆 交与
交与 两点,点
两点,点 .
.
(1)当 时,求
时,求 的值;
的值;
(2)当 时,求
时,求 的取值范围.
的取值范围.
 ,直线
,直线  ,
, 与圆
与圆 交与
交与 两点,点
两点,点 .
.(1)当
 时,求
时,求 的值;
的值;(2)当
 时,求
时,求 的取值范围.
的取值范围.(1)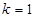 ;(2)
;(2)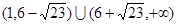 .
.
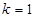 ;(2)
;(2)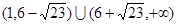 .
.试题分析:(1)由点
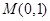 在圆C上且满足
在圆C上且满足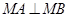 得
得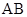 是直径,即直线
是直径,即直线 过圆心
过圆心 ;(2)由
;(2)由 求
求 的取值范围,就是要建立起点
的取值范围,就是要建立起点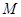 与直线
与直线 的关系,它们是通过点
的关系,它们是通过点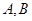 联系起来.我们可以设出
联系起来.我们可以设出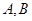 两点的坐标分别为
两点的坐标分别为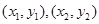 即为
即为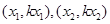 ,一方面由
,一方面由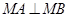 可得到
可得到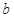 与
与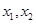 的关系,另一方面直线
的关系,另一方面直线 与圆C相交于点
与圆C相交于点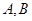 ,把直线方程与圆方程联立方程组,可以得到
,把直线方程与圆方程联立方程组,可以得到 与
与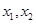 的关系,从而建立起
的关系,从而建立起 与
与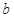 的关系,可求出
的关系,可求出 的范围.
的范围.试题解析:(1)圆的方程可化为
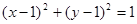 ,故圆心为
,故圆心为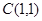 ,半径
,半径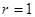 ....2分
....2分当
 时,点
时,点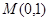 在圆上,又
在圆上,又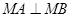 ,故直线
,故直线 过圆心
过圆心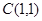 ,∴
,∴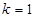 4分
4分从而所求直线
 的方程为
的方程为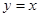 6分
6分(2)设
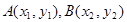 由
由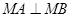 得
得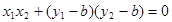 即
即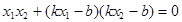
∴
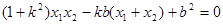 ① 8分
① 8分联立得方程组
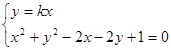 ,化简,整理得
,化简,整理得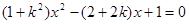 .(*)
.(*)由判别式
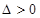 得
得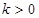 且有
且有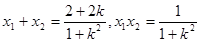 10分
10分代入 ①式整理得
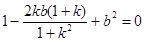 ,从而
,从而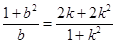 ,又
,又
∴
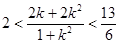 可得
可得 的取值范围是
的取值范围是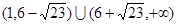 14分
14分
练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
 的距离为
的距离为 ,求该圆的方程.
,求该圆的方程. ,
, ,直线
,直线 (
( 为常数).
为常数).  、
、 到直线
到直线 的距离相等,求实数
的距离相等,求实数 ,
, 恒为锐角,求实数
恒为锐角,求实数 是抛物线
是抛物线 上的点,
上的点, 是
是 的焦点, 以
的焦点, 以 为直径的圆
为直径的圆 与
与 轴的另一个交点为
轴的另一个交点为 .
. 且斜率大于零的直线
且斜率大于零的直线 与抛物线
与抛物线 两点,
两点, 为坐标原点,
为坐标原点, 的面积为
的面积为 ,证明:直线
,证明:直线 (
( )经过圆
)经过圆 的圆心,则
的圆心,则 的最小值是( )
的最小值是( ) 与圆
与圆 :
: 在第一象限内相切于点
在第一象限内相切于点 ,并且分别与
,并且分别与 轴相交于
轴相交于 两点,则
两点,则 的最小值为 .
的最小值为 . 的直线
的直线 被圆
被圆 所截得的弦长为
所截得的弦长为 ,则直线
,则直线 与圆
与圆 相切,则实数
相切,则实数 等于( )
等于( ) 或
或


 相切的直线与
相切的直线与 轴,
轴,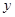 轴的正半轴交于A、B且
轴的正半轴交于A、B且 ,则三角形AOB面积的最小值为 。
,则三角形AOB面积的最小值为 。